题目内容
1.在直线2x-3y+5=0上求点P,使P点到A(2,3)的距离为$\sqrt{13}$,则P点坐标是( )| A. | (5,5) | B. | (-1,1) | C. | (5,5)或(-1,1) | D. | (5,5)或(1,-1) |
分析 利用两点之间的距离公式即可得出.
解答 解:设P(x,y),则y=$\frac{2x+5}{3}$.
由|PA|=$\sqrt{13}$,得(x-2)2+$(\frac{2x+5}{3}-3)^{2}$=13,
即(x-2)2=9.解得x=-1或x=5.
当x=-1时,y=1,当x=5时,y=5,
∴P(-1,1)或P(5,5).
故选:C.
点评 本题考查了两点之间的距离公式,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
16.下列命题中的真命题为( )
| A. | ?x0∈Z,使得1<4x0<3 | B. | ?x0∈Z,使得5x0+1=0 | ||
| C. | ?x∈R,x2-1=0 | D. | ?x∈R,x2+x+2>0 |
6.若10x=3,10y=4,则10x+y的值为( )
| A. | 700 | B. | 300 | C. | 400 | D. | 12 |
11.某人通过普通话二级测试的概率是$\frac{1}{3}$,他连线测试3次,那么其中恰有1次通过的概率是( )
| A. | $\frac{4}{9}$ | B. | $\frac{1}{9}$ | C. | $\frac{4}{27}$ | D. | $\frac{2}{9}$ |
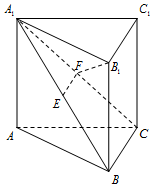 如图,在直三棱柱ABC-A1B1C1中,A1B1⊥B1C1,E、F分别是A1B、A1C的中点.
如图,在直三棱柱ABC-A1B1C1中,A1B1⊥B1C1,E、F分别是A1B、A1C的中点. 如图,在多面体ABCDPE中,四边形ABCD和CDPE都是直角梯形,AB∥DC,∥DC,AD⊥DC,PD⊥平面ABCD,AB=PD=DA=2PE,CD=3PE,F是CE的中点.
如图,在多面体ABCDPE中,四边形ABCD和CDPE都是直角梯形,AB∥DC,∥DC,AD⊥DC,PD⊥平面ABCD,AB=PD=DA=2PE,CD=3PE,F是CE的中点.