题目内容
20. 如图,五面体ABCDE,四边形ABDE是矩形,△ABC是正三角形,AB=1,AE=2,F是线段BC上一点,直线BC与平面ABD所成角为30°,CE∥平面ADF.
如图,五面体ABCDE,四边形ABDE是矩形,△ABC是正三角形,AB=1,AE=2,F是线段BC上一点,直线BC与平面ABD所成角为30°,CE∥平面ADF.(1)试确定F的位置.
(2)求三棱锥A-CDF的体积.
分析 (1)连接AD、BE相交于O,则O为BE的中点,由三角形中位线定理可得OF∥CE,再由线面平行的判定可得CE∥平面ADF;
(2)由F为BC的中点,得VA-CDF=VA-BFD=VF-ABD,由已知求得C到平面ABD的距离为$\frac{1}{2}$,可得F到平面ABD的距离为$\frac{1}{4}$.再求出三角形ABD的面积,代入三棱锥体积公式求得三棱锥A-CDF的体积.
解答 解:(1)如图,四边形ABDE是矩形,连接AD、BE相交于O,则O为BE的中点,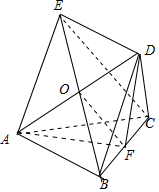
取BC中点F,连接OF,则OF∥CE,
∵OF?平面ADF,CE?平面ADF,∴CE∥平面ADF.
此时F为BC中点;
(2)∵F为BC的中点,∴VA-CDF=VA-BFD=VF-ABD.
∵直线BC与平面ABD所成角为30°,△ABC是正三角形,AB=1,
∴C到平面ABD的距离为$\frac{1}{2}$,F到平面ABD的距离为$\frac{1}{4}$.
又四边形ABDE是矩形,且AE=2,∴${S}_{△ABD}=\frac{1}{2}×1×2=1$.
∴${V}_{F-ABD}=\frac{1}{3}×1×\frac{1}{4}=\frac{1}{12}$.
∴三棱锥A-CDF的体积为$\frac{1}{12}$.
点评 本题考查直线与平面平行的判定,考查了空间想象能力和思维能力,训练了利用等积法求多面体的体积,是中档题.

练习册系列答案
相关题目
8.设k∈Z,函数y=sin ($\frac{π}{4}$+$\frac{x}{2}$)cos ($\frac{π}{4}$+$\frac{x}{2}$)的单调增区间为( )
| A. | [(k+$\frac{1}{2}$)π,(k+1)π] | B. | [(2k+1)π,2(k+1)π] | C. | [kπ,(k+$\frac{1}{2}$)π] | D. | [2kπ,(2k+1)π] |
15.交强险是车主必须为机动车购买的险种.若普通6座以下私家车投保交强险第一年的费用(基准保费)统一为a元,在下一年续保时,实行的是费率浮动机制,保费与上一年度车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就越高,具体浮动情况如表:
某机构为了研究某一品牌普通6座以下私家车的投保情况,随机抽取了60辆车龄已满三年的该品牌同型号私家车的下一年续保时的情况,统计得到了下面的表格:
(Ⅰ)求一辆普通6座以下私家车在第四年续保时保费高于基本保费的频率;
(Ⅱ)某二手车销售商专门销售这一品牌的二手车,且将下一年的交强险保费高于基本保费的车辆记为事故车.假设购进一辆事故车亏损5000元,一辆非事故车盈利10000元,且各种投保类型车的频率与上述机构调查的频率一致,完成下列问题:
①若该销售商店内有六辆(车龄已满三年)该品牌二手车,某顾客欲在店内随机挑选两辆车,求这两辆车中恰好有一辆为事故车的概率;
②若该销售商一次购进120辆(车龄已满三年)该品牌二手车,求一辆车盈利的平均值.
| 交强险浮动因素和浮动费率比率表 | ||
| 浮动因素 | 浮动比率 | |
| A1 | 上一个年度未发生有责任道路交通事故 | 下浮10% |
| A2 | 上两个年度未发生有责任道路交通事故 | 下浮20% |
| A3 | 上三个及以上年度未发生有责任道路交通事故 | 下浮30% |
| A4 | 上一个年度发生一次有责任不涉及死亡的道路交通事故 | 0% |
| A5 | 上一个年度发生两次及两次以上有责任道路交通事故 | 上浮10% |
| A6 | 上一个年度发生有责任道路交通死亡事故 | 上浮30% |
| 类型 | A1 | A2 | A3 | A4 | A5 | A6 |
| 数量 | 10 | 5 | 5 | 20 | 15 | 5 |
(Ⅱ)某二手车销售商专门销售这一品牌的二手车,且将下一年的交强险保费高于基本保费的车辆记为事故车.假设购进一辆事故车亏损5000元,一辆非事故车盈利10000元,且各种投保类型车的频率与上述机构调查的频率一致,完成下列问题:
①若该销售商店内有六辆(车龄已满三年)该品牌二手车,某顾客欲在店内随机挑选两辆车,求这两辆车中恰好有一辆为事故车的概率;
②若该销售商一次购进120辆(车龄已满三年)该品牌二手车,求一辆车盈利的平均值.
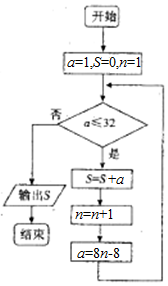 我国古代数学著作《孙子算经》中有如下的问题:“今有方物一束,外周有三十二枚,问积几何?”设每层外周枚数为a,如图是解决该问题的程序框图,则输出的结果为( )
我国古代数学著作《孙子算经》中有如下的问题:“今有方物一束,外周有三十二枚,问积几何?”设每层外周枚数为a,如图是解决该问题的程序框图,则输出的结果为( )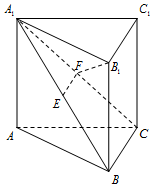 如图,在直三棱柱ABC-A1B1C1中,A1B1⊥B1C1,E、F分别是A1B、A1C的中点.
如图,在直三棱柱ABC-A1B1C1中,A1B1⊥B1C1,E、F分别是A1B、A1C的中点. 如图,在多面体ABCDPE中,四边形ABCD和CDPE都是直角梯形,AB∥DC,∥DC,AD⊥DC,PD⊥平面ABCD,AB=PD=DA=2PE,CD=3PE,F是CE的中点.
如图,在多面体ABCDPE中,四边形ABCD和CDPE都是直角梯形,AB∥DC,∥DC,AD⊥DC,PD⊥平面ABCD,AB=PD=DA=2PE,CD=3PE,F是CE的中点.