题目内容
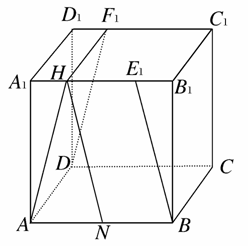
在正三棱柱ABC-A1B1C1中,H、F分别为AB、CC1的中点,各棱长都是4.
(1)求证CH∥平面FA1B.
(2)求证平面ABB1A1⊥平面FA1B.
(3)设E为BB1上一点,试确定E的位置,使HE⊥BC1.
在正三棱柱中,∵H为AB中点,∴CH⊥AB,过H作HM⊥AB交A1B1于M,分别以直线AB、HC、HM为x轴、y轴、z轴建立空间直角坐标系,则B(2,0,0),C(0,2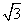 ,0),F(0,2
,0),F(0,2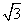 ,2),A(-2,0,0),A1(-2,0,4),C1(0,2
,2),A(-2,0,0),A1(-2,0,4),C1(0,2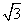 ,4).
,4).
(1)证明:∵ =(0,2
=(0,2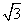 ,0),
,0), =(-2,-2
=(-2,-2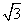 ,2),
,2), =(-2,2
=(-2,2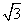 ,2),∴
,2),∴ =
= (
( -
- ),
),
∵ 与
与 不共线,∴
不共线,∴ ∥平面FA1B,
∥平面FA1B,
∵HC⊄平面FA1B,∴HC∥平面FA1B.
(2)证明:平面ABB1A1的一个法向量为n1= =(0,2
=(0,2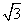 ,0),
,0),
设平面FA1B的一个法向量n=(x,y,z),则
 令x=1得n=(1,0,1),
令x=1得n=(1,0,1),
∵n·n1=0,∴n⊥n1,∴平面ABB1A1⊥平面FA1B.

(3)∵E在BB1上,∴设E(2,0,t),(t>0),则 =(2,0,t),
=(2,0,t), =(-2,2
=(-2,2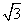 ,4),∵HE⊥BC1,
,4),∵HE⊥BC1,
∴ ·
· =-4+4t=0,∴t=1,
=-4+4t=0,∴t=1,
∴E是BB1上靠近B点的四等分点(或BE= BB1).
BB1).

练习册系列答案
相关题目
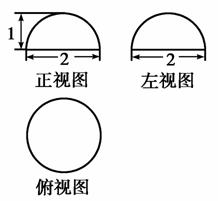
 的值为( )
的值为( ) a2
a2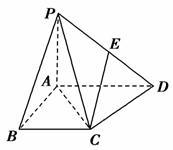

 B.
B.
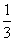 D.
D.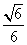
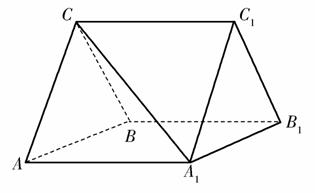
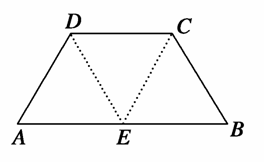
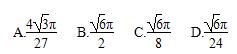
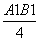 ,求BE1与DF1所成角的余弦值.
,求BE1与DF1所成角的余弦值.