题目内容
如图,四棱锥P-ABCD中,PA⊥平面ABCD,PB与底面所成的角为45°,底面ABCD为直角梯形,∠ABC=∠BAD=90°,PA=BC= AD=1.
AD=1.
(1)求证:平面PAC⊥平面PCD;
(2)在棱PD上是否存在一点E,使CE∥平面PAB?若存在,请确定E点的位置;若不存在,请说明理由.
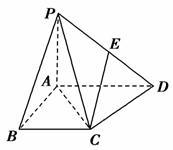
(1)证明:∵PA⊥平面ABCD,
∴PB与平面ABCD所成的角为∠PBA=45°.∴AB=1,
由∠ABC=∠BAD=90°,易得CD=AC=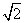 ,∴AC⊥CD.
,∴AC⊥CD.
又∵PA⊥CD,PA∩AC=A,
∴CD⊥平面PAC,又CD⊂平面PCD,
∴平面PAC⊥平面PCD.
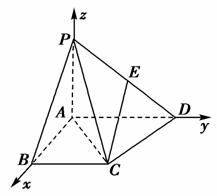
(2)分别以AB、AD、AP为x轴、y轴、z轴建立空间直角坐标系.
∴P(0,0,1),C(1,1,0),D(0,2,0),设E(0,y,z),则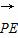 =(0,y,z-1),
=(0,y,z-1),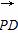 =(0,2,-1).
=(0,2,-1).
∵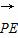 ∥
∥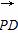 ,
,
∴y·(-1)-2(z-1)=0①
∵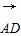 =(0,2,0)是平面PAB的法向量,
=(0,2,0)是平面PAB的法向量,
又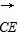 =(-1,y-1,z),CE∥平面PAB.∴
=(-1,y-1,z),CE∥平面PAB.∴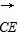 ⊥
⊥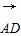 .
.
∴(-1,y-1,z)·(0,2,0)=0,∴y=1.
将y=1代入①,得z= .∴E是PD的中点,
.∴E是PD的中点,
∴存在E点使CE∥平面PAB,此时E为PD的中点.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
 x2上的动点,点P在x轴上的射影为M,点A的坐标是(2,0),则|PA|+|PM|的最小值是________.
x2上的动点,点P在x轴上的射影为M,点A的坐标是(2,0),则|PA|+|PM|的最小值是________.
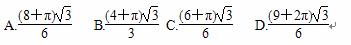

 B.4+
B.4+ D.
D.
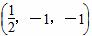 B.(6,-2,-2)
B.(6,-2,-2)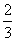 B.
B.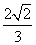
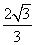 D.
D.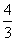
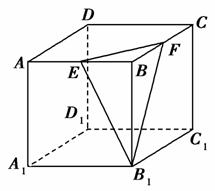
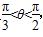 ,则其侧面展开图中心角α满足( )
,则其侧面展开图中心角α满足( )