题目内容
函数y=ax+1+2（a＞0且a≠1）图象一定过点（ ）
| A、（0，2） |
| B、（-1，3） |
| C、（-1，2） |
| D、（0，3） |
考点：指数函数的图像与性质
专题：函数的性质及应用
分析：根据指数函数过定点的性质，直接领x+1=0即可得到结论
解答：
解：由x+1=0，解得x=-1，此时y=1+2=3，
即函数的图象过定点（-1，3），
故选：B
即函数的图象过定点（-1，3），
故选：B
点评：本题主要考查指数函数过定点问题，利用指数幂等于0是解决本题的关键．
练习册系列答案
相关题目
已知函数f（x）=log2（2x+1）的单调增区间是（ ）
| A、（0，+∞） | ||
B、(-
| ||
| C、（-∞，+∞） | ||
D、[
|
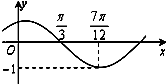函数f（x）=sin（ωx+φ）（其中|φ|＜| π |
| 2 |
A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|
函数f（x）在定义域R上的导函数是f′（x），若f（x）=f（2-x），且当x∈（-∞，1）时，（x-1）f′（x）＜0，设a=f（0、b=f（
）、c=f（log28），则（ ）
| 2 |
| A、a＜b＜c |
| B、a＞b＞c |
| C、c＜a＜b |
| D、a＜c＜b |