题目内容
5.在△ABC中,角A,B,C所对的边分别为a,b,c,且accosB-bccosA=3b2.(1)求$\frac{sinA}{sinB}$的值;
(2)若角C为锐角,c=$\sqrt{11}$,sinC=$\frac{2\sqrt{2}}{3}$,求△ABC的面积.
分析 (1)根据余弦公式求出a2=4b2,根据正弦定理求出$\frac{sinA}{sinB}$的值即可;
(2)求出cosC的值,得到$\frac{{a}^{2}{+b}^{2}-11}{2ab}$=$\frac{1}{3}$以及$\frac{sinA}{sinB}$=$\frac{a}{b}$=2,求出a,b的值,求出三角形的面积即可.
解答 解:(1)∵accosB-bccosA=3b2,
∴$\frac{{a}^{2}{+c}^{2}{-b}^{2}}{2}$-$\frac{{b}^{2}{+c}^{2}{-a}^{2}}{2}$=3b2,
∴a2-b2=3b2,
∴a2=4b2,
∴$\frac{{sin}^{2}A}{{sin}^{2}B}$=4,∴$\frac{sinA}{sinB}$=2;
(2)若角C为锐角,sinC=$\frac{2\sqrt{2}}{3}$,
∴cosC>0,
∴cosC=$\sqrt{1-\frac{8}{9}}$=$\frac{1}{3}$,
∴$\frac{{a}^{2}{+b}^{2}{-c}^{2}}{2ab}$=$\frac{1}{3}$,
∴$\frac{{a}^{2}{+b}^{2}-11}{2ab}$=$\frac{1}{3}$①,
由(1)得,$\frac{sinA}{sinB}$=$\frac{a}{b}$=2②,
联立①②得:b=$\sqrt{3}$,a=2$\sqrt{3}$,
∴S=$\frac{1}{2}$absinC=$\frac{1}{2}$•2$\sqrt{3}$•$\frac{2\sqrt{2}}{3}$=2$\sqrt{2}$.
点评 本题考查了正弦定理以及余弦定理的应用,考查三角形的面积公式,是一道中档题.

 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案| A. | c<a<b | B. | c<b<a | C. | b<a<c | D. | b<c<a |
| A. | 7 | B. | 8 | C. | 15 | D. | 16 |
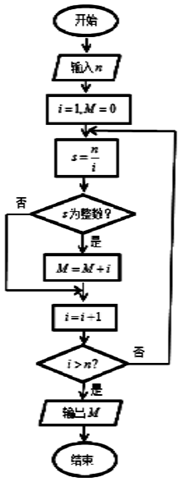 执行如图所示的程序框图,如果输入的n=32,那么输出的M=( )
执行如图所示的程序框图,如果输入的n=32,那么输出的M=( )| A. | 66 | B. | 65 | C. | 64 | D. | 63 |
| 非优良 | 优良 | 总计 | |
| 未设立自习室 | 25 | 15 | 40 |
| 设立自习室 | 10 | 30 | 40 |
| 总计 | 35 | 45 | 80 |
(2)设从该班第一次月考的所有学生的数学成绩中任取2个,取到优良成绩的个数为X,从该班第二次月考的所有学生的数学成绩中任取2个,取到优良成绩的个数为Y,求X与Y的期望并比较大小,请解释所得结论的实际意义.
下面的临界值表供参考:
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |