题目内容
10.某中学是走读中学,为了让学生更有效率利用下午放学后的时间,学校在本学期第一次月考后设立了多间自习室,以便让学生在自习室自主学习、完成作业,同时每天派老师轮流值班.在本学期第二次月考后,高一某班数学老师统计了两次考试该班数学成绩优良人数和非优良人数,得到如下2×2列联表:| 非优良 | 优良 | 总计 | |
| 未设立自习室 | 25 | 15 | 40 |
| 设立自习室 | 10 | 30 | 40 |
| 总计 | 35 | 45 | 80 |
(2)设从该班第一次月考的所有学生的数学成绩中任取2个,取到优良成绩的个数为X,从该班第二次月考的所有学生的数学成绩中任取2个,取到优良成绩的个数为Y,求X与Y的期望并比较大小,请解释所得结论的实际意义.
下面的临界值表供参考:
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
分析 (1)求出K2,与临界值比较,即可得出能在犯错误的概率不超过0.005的前提下认为设立自习室对提高学生成绩有效;
(2)求出期望,即可得出结论.
解答 解:(1)由题意,K2=$\frac{80×(25×30-15×10)^{2}}{40×40×35×45}$=$\frac{80}{7}$>7.879,
∴能在犯错误的概率不超过0.005的前提下认为设立自习室对提高学生成绩有效;
(2)X的取值为0,1,2,则
P(X=0)=$\frac{{C}_{25}^{2}}{{C}_{40}^{2}}$=$\frac{5}{13}$,P(X=1)=$\frac{{C}_{25}^{1}{C}_{15}^{1}}{{C}_{40}^{2}}$=$\frac{25}{52}$,P(X=2)=$\frac{{C}_{15}^{2}}{{C}_{40}^{2}}$=$\frac{7}{52}$,
∴E(X)=0×$\frac{5}{13}+1×\frac{25}{52}+2×\frac{7}{52}$=$\frac{3}{4}$.
Y的取值为0,1,2,则:
P(Y=0)=$\frac{{C}_{10}^{2}}{{C}_{40}^{2}}$=$\frac{3}{52}$,P(Y=1)=$\frac{{C}_{10}^{1}{C}_{30}^{1}}{{C}_{40}^{2}}$=$\frac{5}{13}$,P(Y=2)=$\frac{{C}_{30}^{2}}{{C}_{40}^{2}}$=$\frac{29}{52}$,
E(Y)=$0×\frac{3}{52}+1×\frac{5}{13}+2×\frac{29}{52}$=$\frac{3}{2}$.
也即EX<EY,其实际含义即表明设立自习室有效.
点评 本题主要考查概率与统计的应用,利用条件建立随机变量的分布列,考查学生的运算能力,综合性较强.

| A. | 30° | B. | 45° | C. | 60° | D. | 120° |
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
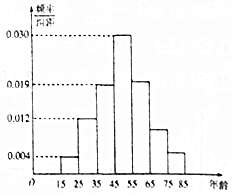 2016年双十一活动结束后,某地区研究人员为了研究该地区在双十一活动中消费超过3000元的人群的年龄状况,随机在当地消费超过3000元的群众中抽取了500人作调查,所得频率分布直方图如图所示:
2016年双十一活动结束后,某地区研究人员为了研究该地区在双十一活动中消费超过3000元的人群的年龄状况,随机在当地消费超过3000元的群众中抽取了500人作调查,所得频率分布直方图如图所示: