题目内容
15.已知椭圆E:x2+3y2=m2(m>0)的左顶点是A,左焦点为F,上顶点为B.(1)当△AFB的面积为$\frac{\sqrt{3}-\sqrt{2}}{2}$时,求m的值;
(2)若直线l交椭圆E于M,N两点(不同于A),以线段MN为直径的圆过A点,试探究直线l是否过定点,若存在定点,求出这个定点的坐标,若不存在定点,请说明理由.
分析 (1)将椭圆方程转化成标准方程,则三角形AFB的面积S=$\frac{1}{2}$b×(b-c),代入即可求得m的值;
(2)设直线AM的方程,代入椭圆方程,利用韦达定理求得M和N的方程,当l的斜率不存在时,显然可得k=1,求得圆心为P(-$\frac{m}{2}$,0),当l的斜率存在时,由利用两点的斜率公式求得kPM=kPN,直线l是否过定点.
解答 解:(1)由椭圆方程:$\frac{{x}^{2}}{{m}^{2}}+\frac{{y}^{2}}{\frac{{m}^{2}}{3}}=1$,则a=m,b=$\frac{m}{\sqrt{3}}$,c=$\frac{\sqrt{2}m}{\sqrt{3}}$,
由三角形AFB的面积S,S=$\frac{1}{2}$b×(b-c)=$\frac{\sqrt{3}-\sqrt{2}}{2}$,
则$\frac{m}{\sqrt{3}}$(m-$\frac{\sqrt{2}m}{\sqrt{3}}$)$\sqrt{3}$-$\sqrt{2}$,解得:m=$\sqrt{3}$,
∴m的值为$\sqrt{3}$;
(2)由线段MN过直径的圆过A点,则MA⊥NA,
设直线AM的斜率为k(k>0),则直线AN的斜率为-$\frac{1}{k}$,AM为y=k(x+m),
设A(x1,y1),B(x2,y2),则$\left\{\begin{array}{l}{y=k(x+m)}\\{{x}^{2}+3{y}^{2}={m}^{2}}\end{array}\right.$,
整理得:(3k2+1)x2+6k2mx+(3k2-1)m2=0,
则x1(-m)=$\frac{{(3{k}^{2}-1)m}^{2}}{3{k}^{2}+1}$,则x1=$\frac{m(1-3{k}^{2})}{3{k}^{2}+1}$,故y1=k(x1+m)=$\frac{2mk}{3{k}^{2}+1}$,
则M($\frac{m(1-3{k}^{2})}{3{k}^{2}+1}$,$\frac{2mk}{3{k}^{2}+1}$),
直线AN的方程为y=-$\frac{1}{k}$(x+m),同理可得:N($\frac{m({k}^{2}-3)}{{k}^{2}+3}$,-$\frac{2mk}{{k}^{2}+3}$),
当l的斜率不存在时,显然可得k=1,此时M(-$\frac{m}{2}$,$\frac{m}{2}$),N(-$\frac{m}{2}$,-$\frac{m}{2}$),
则圆心为P(-$\frac{m}{2}$,0),
由直线l总穿过x轴,证明当l的斜率存在时,也过点P(-$\frac{m}{2}$,0),
当l的斜率存在时,kPM=$\frac{\frac{2mk}{3{k}^{2}+1}-0}{\frac{m(1-3{k}^{2})}{3{k}^{2}+1}+\frac{m}{2}}$=$\frac{4k}{3(1-{k}^{2})}$=kPN(k>0,k≠1),
综上可知:l过定点(-$\frac{m}{2}$,0).
点评 本题考查椭圆的标准方程及简单简单几何性质,考查直线与椭圆的位置关系,考查韦达定理,直线的斜率公式,考查计算能力,属于中档题.

| A. | (-$\frac{π}{2}$,1) | B. | (-$\frac{π}{12}$,1) | C. | ($\frac{π}{6}$,1) | D. | ($\frac{π}{4}$,0) |

| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
| A. | $\frac{π}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{3}{4}π$ | D. | $\frac{2}{3}π$ |
| A. | 3 | B. | 6 | C. | 3$\sqrt{3}$ | D. | 6$\sqrt{3}$ |
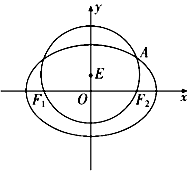 如图,已知圆E:${x^2}+{({y-\frac{1}{2}})^2}=\frac{9}{4}$经过椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的左右焦点F1,F2,与椭圆C在第一象限的交点为A,且F1,E,A三点共线.
如图,已知圆E:${x^2}+{({y-\frac{1}{2}})^2}=\frac{9}{4}$经过椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的左右焦点F1,F2,与椭圆C在第一象限的交点为A,且F1,E,A三点共线.