题目内容
5．已知数列{an}的前n项和${S_n}={n^2}-7n+3$，则有（ ）| A． | S3最小 | B． | S4最小 | C． | S7最小 | D． | S3，S4最小 |
分析 根据一元二次函数的性质进行转化求解即可．
解答 解：${S_n}={n^2}-7n+3$的对称轴为n=$-\frac{-7}{2}$=$\frac{7}{2}$，
∴当n=3或n=4时，Sn取得最小值，
故选：D
点评 本题主要考查数列前n项和公式的应用，根据一元二次函数的性质是解决本题的关键．
练习册系列答案
相关题目
15．为了在运行右面的程序之后输出y=2，输入的x可以是（ ）
| A． | 0 | B． | 2 | C． | 0或2 | D． | -1，0或2 |
13．过点A（4，a）和B（5，b）的直线与直线y=2x+m平行，则|AB|=（ ）
| A． | 2 | B． | $\sqrt{2}$ | C． | 5 | D． | $\sqrt{5}$ |
20．已知直线ax-ky+k=0（a为常数，k≠0为参数），不论k取何值，直线总过定点（ ）
| A． | （a，0） | B． | （1，0） | C． | （1，1） | D． | （0，1） |
10．已知O为坐标原点，F是椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$的左焦点，A、B分别为椭圆C的左、右顶点，P为椭圆C上一点，且PF⊥x轴．过顶点A的直线l与线段PF交于点M，与y轴交于点E．若直线BM经过OE的中点，则椭圆C的离心率为（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{1}{4}$ | C． | $\frac{2}{3}$ | D． | $\frac{3}{4}$ |
17．设点A（3，-5），B（-2，-2），直线l过点P（1，1）且与线段AB相交，则直线l的斜率k的取值范围是（ ）
| A． | k≥1或k≤-3 | B． | -3≤k≤1 | C． | -1≤k≤3 | D． | 以上都不对 |
14．
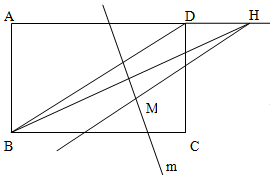如图所示，ABCD是长为8，宽为4的矩形，设点H在直线AD上运动，BH的垂直平分线为m，过点H且与BD平行（或重合）的直线与直线m相交于点M，则点M的轨迹为（ ）
如图所示，ABCD是长为8，宽为4的矩形，设点H在直线AD上运动，BH的垂直平分线为m，过点H且与BD平行（或重合）的直线与直线m相交于点M，则点M的轨迹为（ ）| A． | 圆的一部分 | B． | 椭圆的一部分 | C． | 双曲线的一部分 | D． | 抛物线的一部分 |
15．
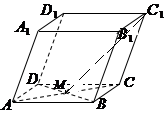四棱柱ABCD-A1B1C1D1的底面是平行四边形，M是AC与BD的交点．若$\overrightarrow{AB}$=$\overrightarrow a$，$\overrightarrow{AD}$=$\overrightarrow b$，$\overrightarrow{A{A_1}}$=$\overrightarrow c$，则$\overrightarrow{{C_1}M}$可以表示为（ ）
四棱柱ABCD-A1B1C1D1的底面是平行四边形，M是AC与BD的交点．若$\overrightarrow{AB}$=$\overrightarrow a$，$\overrightarrow{AD}$=$\overrightarrow b$，$\overrightarrow{A{A_1}}$=$\overrightarrow c$，则$\overrightarrow{{C_1}M}$可以表示为（ ）| A． | $\overrightarrow a+\overrightarrow b+\frac{1}{2}\overrightarrow c$ | B． | $-\frac{1}{2}\overrightarrow a-\frac{1}{2}\overrightarrow b+\overrightarrow c$ | C． | $-\frac{1}{2}\overrightarrow a-\frac{1}{2}\overrightarrow b-\overrightarrow c$ | D． | $\frac{1}{2}\overrightarrow a+\frac{1}{2}\overrightarrow b+\overrightarrow c$ |