题目内容
17.设i是虚数单位,若复数$a+\frac{5i}{1-2i}({a∈R})$是纯虚数,则a=( )| A. | -1 | B. | 1 | C. | -2 | D. | 2 |
分析 利用复数代数形式的乘除运算化简,然后由实部等于0求得a值.
解答 解:∵$a+\frac{5i}{1-2i}=a+\frac{5i(1+2i)}{(1-2i)(1+2i)}$=$a+\frac{-10+5i}{5}=a-2+i$是纯虚数,
∴a=2.
故选:D.
点评 本题考查复数代数形式的乘除运算,考查了复数的基本概念,是基础题.

练习册系列答案
相关题目
7.已知集合M={x∈N|x2-5x-6<0},N={x∈Z|2<x<23},则M∩N=( )
| A. | (2,6) | B. | {3,4,5} | C. | {2,3,4,5,6} | D. | [2,6] |
8.已知函数f(x)=$\left\{\begin{array}{l}{ln(x+1),x≥0}\\{-x{e}^{x},x<0}\end{array}\right.$,方程f2(x)+mf(x)=0(m∈R)有四个不相等的实数根,则实数m的取值范围是( )
| A. | (-∞,-$\frac{1}{e}$) | B. | (-$\frac{1}{e}$,0) | C. | (-$\frac{1}{e}$,+∞) | D. | (0,$\frac{1}{e}$) |
2.若函数$f(x)=\left\{\begin{array}{l}2x+2,x≤0\\{2^x}-4,x>0\end{array}\right.$,则f(f(1))的值为( )
| A. | -10 | B. | 10 | C. | -2 | D. | 2 |
9.集合A={x|x2-2x-8≤0},B={x|2x<8},则A∩B=( )
| A. | (-∞,2] | B. | [-2,3) | C. | [-4,3) | D. | (-∞,3] |
7.设定义在D上的函数y=h(x)在点P(x0,h(x0))处的切线方程为l:y=g(x),当x≠x0时,若$\frac{h(x)-g(x)}{x-{x}_{0}}$>0在D内恒成立,则称P为函数y=h(x)的“类对称点”,则f(x)=lnx+x2-x的“类对称点”的横坐标是( )
| A. | 2 | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
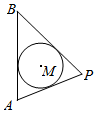 某建筑工地在施工过程中,为了保护一口直径为1米的圆形古井M,决定将其围起来,工地上现有一块长为2米(宽为1.2米)的木工板AB可利用,现将其围成高1.2米的围挡,如图,圆M与AB,PA,PB(PA,PB为另外两侧的围挡)均相切.
某建筑工地在施工过程中,为了保护一口直径为1米的圆形古井M,决定将其围起来,工地上现有一块长为2米(宽为1.2米)的木工板AB可利用,现将其围成高1.2米的围挡,如图,圆M与AB,PA,PB(PA,PB为另外两侧的围挡)均相切.