题目内容
9.已知下列四个关系:①a>b?ac2>bc2;
②a>b⇒$\frac{1}{a}$<$\frac{1}{b}$;
③a>b>0,c>d⇒$\frac{a}{d}$>$\frac{b}{c}$;
④a>b>0⇒ac<bc.
其中正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 取特殊值判断①②③,根据指数函数的性质判断④.
解答 解:对于①c=0时,不成立,故①错误;
对于②令a=1,b=-1,不成立,故②错误;
对于③令a=1,b=-1,不成立,故③错误;
对于④,由于a>b>1,当x<0时,ax<bx,
故ac<bc正确,
故选:A.
点评 本题考查了不等式的性质,考查特殊值法的应用,是一道基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.ω是正实数,函数f(x)=2cosωx在x∈$[{0,\frac{2π}{3}}]$上是减函数,且有最小值1,那么ω的值可以是( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | 3 |
18.若z=$\frac{\sqrt{2}}{1-i}$,那么z100的值为( )
| A. | 1 | B. | -1 | C. | -i | D. | i |
19.已知x1>0,x1≠1且xn+1=$\frac{{{x_n}(x_n^2+3)}}{3x_n^2+1}$(n=1,2,…).试证:“在数列{xn}中,对任意正整数n都满足xn<xn+1”,当此题用反证法证明,否定结论时,应为( )
| A. | 对任意的正整数n,有xn=xn+1 | B. | 存在正整数n,使xn=xn+1 | ||
| C. | 存在正整数n,使xn≥xn+1 | D. | 存在正整数n,使xn-xn-1≥0 |
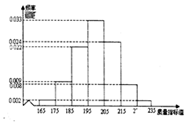 从某企业的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得如下频率分布直方图:
从某企业的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得如下频率分布直方图: