题目内容
1.设f(x)是定义在R上的奇函数,且f(x)=2x+$\frac{m}{{2}^{x}}$,设g(x)=$\left\{\begin{array}{l}{f(x),x>1}\\{f(-x),x≤1}\end{array}\right.$.若函数y=g(x)-t有且只有一个零点,则实数t的取值范围是[-$\frac{3}{2}$,$\frac{3}{2}$].分析 根据函数奇偶性的性质,利用f(0)=0求出m的值,利用g(x)与f(x)的关系求出g(x)的表达式,利用函数与方程的关系转化为两个函数的交点个数问题,利用数形结合进行求解即可.
解答 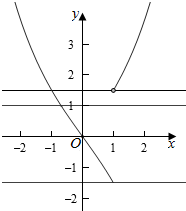 解:∵f(x)是定义在R上的奇函数,且f(x)=2x+$\frac{m}{{2}^{x}}$,
解:∵f(x)是定义在R上的奇函数,且f(x)=2x+$\frac{m}{{2}^{x}}$,
∴f(0)=0,即f(0)=1+m=0,得m=-1,
则f(x)=2x-$\frac{1}{{2}^{x}}$,
则g(x)=$\left\{\begin{array}{l}{{2}^{x}-\frac{1}{{2}^{x}},}&{x>1}\\{\frac{1}{{2}^{x}}-{2}^{x},}&{x≤1}\end{array}\right.$,
则当x>1时,函数为增函数,且当x→1时,g(x)→${2}^{1}-\frac{1}{{2}^{1}}$=2-$\frac{1}{2}$=$\frac{3}{2}$,
当x≤1时,函数为减函数,且g(x)≥g(1)=-(${2}^{1}-\frac{1}{{2}^{1}}$)=$\frac{1}{2}$-2=-$\frac{3}{2}$,
由y=g(x)-t=0得g(x)=t,
作出函数g(x)和y=t的图象如图:
要使函数y=g(x)-t有且只有一个零点,
则函数g(x)与y=t只有一个交点,
则-$\frac{3}{2}$≤t≤$\frac{3}{2}$,
故答案为:[-$\frac{3}{2}$,$\frac{3}{2}$]
点评 本题主要考查函数与方程的应用,利用函数与方程的关系转化为两个函数的交点个数问题,利用数形结合是解决本题的关键.

练习册系列答案
相关题目
12.已知复数z(1+i)=2i,则复数z=( )
| A. | 1+i | B. | 1-i | C. | $\frac{1}{2}$+$\frac{1}{2}$i | D. | $\frac{1}{2}$-$\frac{1}{2}$i |
9.在复平面内,复数z=$\frac{2-i}{i}$的共轭复数$\overline{z}$对应的点所在的象限( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
16.已知数列{an}的前n项和为Sn,a1=1,Sn=2an+1,则当n>1时,Sn=( )
| A. | ($\frac{3}{2}$)n-1 | B. | 2n-1 | C. | ($\frac{2}{3}$)n-1 | D. | $\frac{1}{3}$($\frac{1}{{2}^{n-1}}$-1) |
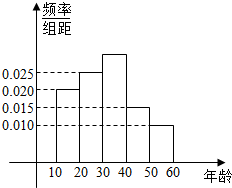 某市在“国际禁毒日”期间,连续若干天发布了“珍爱生命,原理毒品”的电视公益广告,期望让更多的市民知道毒品的危害性,禁毒志愿者为了了解这则广告的宣传效果,随机抽取了100名年龄阶段性在[10,20),[20,30),[30,40),[40,50),[50,60)的市民进行问卷调查,由此得到样本频率分布直方图如图所示.
某市在“国际禁毒日”期间,连续若干天发布了“珍爱生命,原理毒品”的电视公益广告,期望让更多的市民知道毒品的危害性,禁毒志愿者为了了解这则广告的宣传效果,随机抽取了100名年龄阶段性在[10,20),[20,30),[30,40),[40,50),[50,60)的市民进行问卷调查,由此得到样本频率分布直方图如图所示.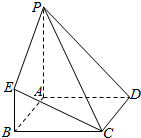 在如图所示的几何体中,四边形ABCD为正方形,PA⊥平面ABCD,PA∥BE,AB=PA=6,BE=3.
在如图所示的几何体中,四边形ABCD为正方形,PA⊥平面ABCD,PA∥BE,AB=PA=6,BE=3.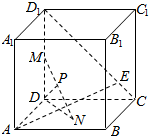 已知棱长为3的正方体ABCD-A1B1C1D1中,长为2的线段MN的一端点M在DD1上运动,另一个端点N在底面ABCD上运动,动点E在线段CD1上,则MN中点P到线段AE距离的最小值为$\sqrt{3}-1$.
已知棱长为3的正方体ABCD-A1B1C1D1中,长为2的线段MN的一端点M在DD1上运动,另一个端点N在底面ABCD上运动,动点E在线段CD1上,则MN中点P到线段AE距离的最小值为$\sqrt{3}-1$.