题目内容
3．设函数f（x）=ax+sinx+cosx．若函数f（x）的图象上存在不同的两点A、B，使得曲线y=f（x）在点A、B处的切线互相垂直，则实数a的取值范围为（ ）| A． | $[-\frac{1}{2}，\frac{1}{2}]$ | B． | $[-\sqrt{2}，\sqrt{2}]$ | C． | $（-∞，-\sqrt{2}）∪（\sqrt{2}，+∞）$ | D． | [-1，1] |
分析 求出原函数的导函数，设出A，B的坐标，代入导函数，由函数在A，B处的导数等于0列式，换元后得到关于a的一元二次方程，结合线性规划知识求得a的取值范围．
解答 解：由f（x）=ax+sinx+cosx，得f′（x）=a+cosx-sinx，
设A（x1，y1），B（x2，y2），
则f′（x1）=a+cosx1-sinx1，f′（x2）=a+cosx2-sinx2．
由曲线y=f（x）在点A、B处的切线互相垂直，得
a2+[（cosx1-sinx1）+（cosx2-sinx2）]a+（cosx1-sinx1）（cosx2-sinx2）+1=0．
令m=cosx1-sinx1，n=cosx2-sinx2，
则m∈[-$\sqrt{2}$，$\sqrt{2}$]，n∈[-$\sqrt{2}$，$\sqrt{2}$]，
∴a2+（m+n）a+mn+1=0．
△=（m+n）2-4mn-4=（m-n）2-4，
∴0≤（m-n）2-4≤4．
当m-n=$±2\sqrt{2}$时，m+n=0，
又a=$\frac{-（m+n）±\sqrt{（m-n）^{2}-4}}{2}$．
∴-1≤a≤1．
∴函数f（x）的图象上存在不同的两点A，B，
使得曲线y=f（x）在点A，B处的切线互相垂直，则实数a的取值范围为[-1，1]．
故选D．
点评 本题考查利用导数研究曲线上某点的切线方程，考查了数学转化思想方法，解答的关键在于由关于a的方程的根求解a的范围，是有一定难度题目．
练习册系列答案
相关题目
13．化简$\frac{cos2α}{{4{{sin}^2}（\frac{π}{4}+α）tan（\frac{π}{4}-α）}}$=（ ）
| A． | cosα | B． | sinα | C． | 1 | D． | $\frac{1}{2}$ |
14．已知函数$f（x）=sin（\frac{π}{3}x+φ）（|φ|＜\frac{π}{2}）$的图象关于直线x=1对称，把f（x）的图象向右平移3个单位长度后，所得图象对应的函数解析式为（ ）
| A． | y=sin（$\frac{π}{3}$x+$\frac{π}{6}$） | B． | y=sin（$\frac{π}{3}$x-$\frac{π}{6}$） | C． | y=cos（$\frac{π}{3}$x+$\frac{π}{6}$） | D． | y=sin（$\frac{π}{3}$x-$\frac{5π}{6}$） |
11．一条光线从点（-2，-3）射出，经y轴反射后与圆（x+3）2+（y-2）2=1相切，则入射光线所在直线的斜率为（ ）
| A． | $\frac{3}{2}$或$\frac{2}{3}$ | B． | $\frac{4}{3}$或$\frac{3}{4}$ | C． | $\frac{5}{3}或\frac{3}{5}$ | D． | $\frac{5}{4}或\frac{4}{5}$ |
18．“函数f（x）=ax+3在（-1，2）上存在零点”是“3＜a＜4”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
8．直线x-y=0与圆x2+y2=1的位置关系是（ ）
| A． | 相切 | B． | 相离 | ||
| C． | 相交且直线过圆心 | D． | 相交且直线不过圆心 |
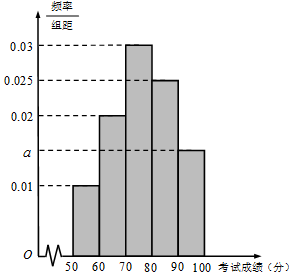某市为了了解本市高中学生的汉字书写水平，在全市范围内随机抽取了近千名学生参加汉字听写考试，将所得数据进行分组，分组区间为：[50，60），[60，70），[70，80），[80，90），[90，100]，并绘制出频率分布直方图，如图所示．