题目内容
已知△ABC的角A、B、C所对的边分别是a、b、c，设向量m＝(a，b)，n＝(sin B，sin A)，p＝(b－2，a－2)．
(1) 若m∥n，求证：△ABC为等腰三角形；
(2) 若m⊥p，边长c＝2，角C＝
，求△ABC的面积．
(1) 证明：∵ m∥n，∴ asin A＝bsin B，即a·
＝b·
，其中R是△ABC外接圆半径，∴ a＝b.∴ △ABC为等腰三角形．
(2) 解：由题意可知m·p＝0，即a(b－2)＋b(a－2)＝0.∴ a＋b＝ab.由余弦定理可知，4＝a2＋b2－ab＝(a＋b)2－3ab，即(ab)2－3ab－4＝0，∴ab＝4(舍去ab＝－1)，
∴ S＝
absin C＝×4×sin ＝
.
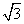练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
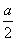(n2－n＋2)万元，乙超市第n年的销售额比前一年销售额多
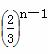a万元．
则A＝________．
，x∈R，A>0，0<φ<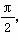
，y＝f(x)的部分图象如图所示，P、Q分别为该图象的最高点和最低点，点P的坐标为(1，A)．
，求A的值．
＋θ)＝
，则cos2θ＝________．
＝
π＜x＜
π，求
的值．
＝
，tan
＝
，则tan(α＋β)＝________．