题目内容
7.学校要安排一场文艺晚会的11个节目的演出顺序,除第1个节目和最后1个节自己确定外,还有4个音乐节目,3个舞蹈节目,2个曲艺节目,目3个舞蹈节目要求不能相邻,2个曲艺节目出场前后顺序已定,共有多少种不同排法?分析 先把4个音乐节目,2个曲艺节目,经行全排,且2个曲艺节目出场前后顺序已定,形成了7个空,选3个,把舞蹈节目插入即可.
解答 解:先把4个音乐节目,2个曲艺节目,经行全排,且2个曲艺节目出场前后顺序已定,形成了7个空,选3个,把舞蹈节目插入,
故有$\frac{1}{2}$A66A73=75600种.
点评 本题主要考查排列组合两个基本原理的实际应用,本题解题的关键是对于有限制的元素要优先排,不相邻的问题一般都用“插空法”,属于中档题.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
2.已知复数z1,z2,则下列说法中正确的是( )
| A. | |z1|+|z2|>|z1+z2| | B. | |z1|-|z2|>|z1-z2| | C. | |z1|+|z2|≥|z1+z2| | D. | |z1|-|z2|≥|z1-z2| |
12.设n,m∈N,n>m,则下列等式中不正确的是( )
| A. | ${C}_{n}^{m}$=${C}_{n}^{n-m}$ | B. | ${C}_{m}^{m}$+${C}_{m}^{m-1}$=${C}_{m+1}^{m}$ | ||
| C. | ${C}_{5}^{1}$+${C}_{5}^{2}$=${C}_{5}^{3}$ | D. | ${C}_{n+1}^{m}$=${C}_{n}^{m-1}$+${C}_{n-1}^{m}$+${C}_{n-1}^{m-1}$ |
 如图,在三棱柱ABM-DCN中,侧面ADNM⊥侧面ABCD,且侧面ADNM是矩形,AD=2,AM=1,侧面ABCD是菱形,∠DAB=60°,E是AB的中点.
如图,在三棱柱ABM-DCN中,侧面ADNM⊥侧面ABCD,且侧面ADNM是矩形,AD=2,AM=1,侧面ABCD是菱形,∠DAB=60°,E是AB的中点.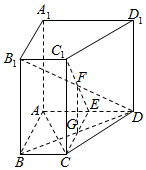 如图,在四棱柱ABCD-A1B1C1D1中,AC⊥B1D,BB1⊥底面ABCD,E为线段AD上的任意一点(不包括A、D两点),平面CEC1与平面BB1D交于FG.
如图,在四棱柱ABCD-A1B1C1D1中,AC⊥B1D,BB1⊥底面ABCD,E为线段AD上的任意一点(不包括A、D两点),平面CEC1与平面BB1D交于FG.