题目内容
1.已知曲线C:$\left\{\begin{array}{l}{x=-3+4cosθ}\\{y=4+4sinθ}\end{array}\right.$(θ为参数),直线l1:kx-y+k=0,l2:cosθ-2sinθ=$\frac{4}{ρ}$(Ⅰ)写出曲线C和直线l2的普通方程;
(Ⅱ)l1与C交于不同两点M,N,MN的中点为P,l1与l2的交点为Q,l1恒过点A,求|AP|•|AQ|
分析 (Ⅰ)利用三种方程的转化方法,即可写出曲线C和直线l2的普通方程;
(Ⅱ)l1的参数方程$\left\{\begin{array}{l}{x=-1+tcosα}\\{y=tsinα}\end{array}\right.$代入圆C方程、l2的方程,利用参数的几何意义,即可得出结论.
解答 解:(Ⅰ)曲线C:$\left\{\begin{array}{l}{x=-3+4cosθ}\\{y=4+4sinθ}\end{array}\right.$(θ为参数),普通方程为(x+3)2+(y-4)2=16;
l2:cosθ-2sinθ=$\frac{4}{ρ}$普通方程为x-2y-4=0;
(Ⅱ)l1的参数方程$\left\{\begin{array}{l}{x=-1+tcosα}\\{y=tsinα}\end{array}\right.$代入圆C方程可得t2+4(cosα-2sinα)t-12=0,
t1+t2=-4(cosα-2sinα),
∴|AP|=$\frac{1}{2}$|t1+t2|=|2(cosα-2sinα)|
代入l2的方程,可得t=|AQ|=|$\frac{5}{cosα-2sinα}$|,
∴|AP|•|AQ|=10.
点评 本题考查三种方程的转化,考查参数方程的运用,考查参数的几何意义,属于中档题.

练习册系列答案
相关题目
13.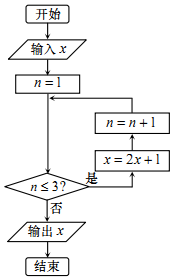 已知实数 x∈[1,10],执行如图所示的程序框图,则输出的x不大于63的概率为( )
已知实数 x∈[1,10],执行如图所示的程序框图,则输出的x不大于63的概率为( )
 已知实数 x∈[1,10],执行如图所示的程序框图,则输出的x不大于63的概率为( )
已知实数 x∈[1,10],执行如图所示的程序框图,则输出的x不大于63的概率为( )| A. | $\frac{3}{10}$ | B. | $\frac{1}{3}$ | C. | $\frac{3}{5}$ | D. | $\frac{2}{3}$ |
16.已知函数f(x)=2sin(ωx+$\frac{π}{6}$)(ω>0)的周期为π,则下列选项正确的是( )
| A. | 函数f(x)的图象关于点($\frac{π}{6}$,0)对称 | B. | 函数f(x)的图象关于点(-$\frac{π}{12}$,0)对称 | ||
| C. | 函数f(x)的图象关于直线x=$\frac{π}{3}$对称 | D. | 函数f(x)的图象关于直线x=-$\frac{π}{12}$对称 |
13.李冶(1192-1279),真定栾城(今属河北石家庄市)人,金元时期的数学家、诗人、晚年在封龙山隐居讲学,数学著作多部,其中《益古演段》主要研究平面图形问题:求圆的直径,正方形的边长等,其中一问:现有正方形方田一块,内部有一个圆形水池,其中水池的边缘与方田四边之间的面积为13.75亩,若方田的四边到水池的最近距离均为二十步,则圆池直径和方田的边长分别是(注:240平方步为1亩,圆周率按3近似计算)( )
| A. | 10步、50步 | B. | 20步、60步 | C. | 30步、70步 | D. | 40步、80步 |
10.在复平面中,复数$\frac{1}{(1+i)^{2}+1}$对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
11.已知正项等差数列{an}中,a1+a2+a3=15,若a1+2,a2+5,a3+13成等比数列,则a10=( )
| A. | 21 | B. | 22 | C. | 23 | D. | 24 |
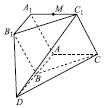 如图,已知平面ADC∥平面A1B1C1,B为线段AD的中点,△ABC≈△A1B1C1,四边形ABB1A1为正方形,平面AA1C1C丄平面ADB1A1,A1C1=A1A,∠C1A1A=$\frac{π}{3}$,M为棱A1C1的中点.
如图,已知平面ADC∥平面A1B1C1,B为线段AD的中点,△ABC≈△A1B1C1,四边形ABB1A1为正方形,平面AA1C1C丄平面ADB1A1,A1C1=A1A,∠C1A1A=$\frac{π}{3}$,M为棱A1C1的中点.