题目内容
3．已知集合$M=\{x|y=\sqrt{-{x^2}+2x+8}\}$，集合N={y|y=|x|+1}，则M∩N=（ ）| A． | {x|-2≤x≤4} | B． | {x|x≥1} | C． | {x|1≤x≤4} | D． | {x|x≥-2} |
分析 求出M中x的范围确定出M，求出N中y的范围确定出N，找出M与N的交集即可．
解答 解：由M中-x2+2x+8≥0，即x2-2x-8≤0，即（x-4）（x+2）≤0，解得-2≤x≤4，即M={x|-2≤x≤4}，
集合N={y|y=|x|+1}=[1，+∞），
则M∩N={x|1≤x≤4}
故选：C
点评 此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．
练习册系列答案
相关题目
如图，四棱锥P-ABCD 中，∠ABC=∠BAD=90°，BC=2AD，△PAB与△PAD 都是边长为2的等边三角形，E 是BC的中点．
14．执行如图所示的程序框图，则输出的s的值是（ ）
| A． | 7 | B． | 6 | C． | 5 | D． | 3 |
11．设随机变量ξ服从正态分布N（μ，7），若P（ξ＜2）=P（ξ＞4），则μ 与Dξ的值分别为（ ）
| A． | $μ=\sqrt{3}，Dξ=\sqrt{7}$ | B． | $μ=\sqrt{3}，Dξ=7$ | C． | μ=3，Dξ=7 | D． | $μ=3，Dξ=\sqrt{7}$ |
18．
某程序框图如图所示，其中$g（x）=\frac{1}{{{x^2}+x}}$，若输出的$S=\frac{2016}{2017}$，则判断框内应填入的条件为（ ）
某程序框图如图所示，其中$g（x）=\frac{1}{{{x^2}+x}}$，若输出的$S=\frac{2016}{2017}$，则判断框内应填入的条件为（ ）| A． | n＜2017 | B． | n≤2017 | C． | n＞2017 | D． | n≥2017 |
12．已知集合A={x|1＜x＜3}，B={x|x＞2}，则A∪∁RB=（ ）
| A． | {x|x≤2} | B． | {x|2＜x＜3} | C． | {x|x＜3} | D． | {x|1＜x≤2} |
13．
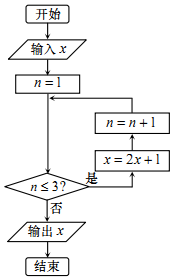已知实数 x∈[1，10]，执行如图所示的程序框图，则输出的x不大于63的概率为（ ）
已知实数 x∈[1，10]，执行如图所示的程序框图，则输出的x不大于63的概率为（ ）| A． | $\frac{3}{10}$ | B． | $\frac{1}{3}$ | C． | $\frac{3}{5}$ | D． | $\frac{2}{3}$ |