Question

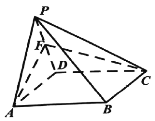
【题目】如图，将等腰直角三角形沿斜边上的高翻折，使二面角的大小为，翻折后的中点为.

（Ⅰ）证明平面；

（Ⅱ）求二面角的余弦值.

Answer 1

【答案】（Ⅰ）证明见解析；（Ⅱ）.

【解析】

（Ⅰ）根据等腰直角三角形沿斜边上的高翻折，则， ，又是的中点，易得，，再利用线面垂直的判定定理证明.

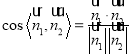（Ⅱ）建立空间直角坐标系，不妨设，易知二面角的平面角是，则，然后分别求得平面的一个法向量，平面的一个法向量，代入公式求解..

（Ⅰ）∵折叠前，是斜边上的高，

∴是的中点，

∴，又因为折叠后是的中点，

∴，折叠后，

∴，，

∴平面；

（Ⅱ）建立如图空间直角坐标系，

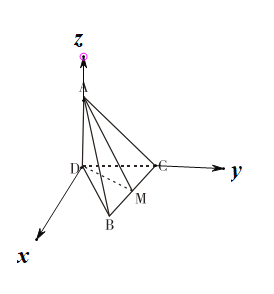
不妨设，易知二面角的平面角是，

则，

∴，，，，

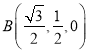设平面的一个法向量为，

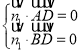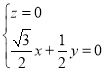得，即，令,

得，

设平面的一个法向量,

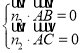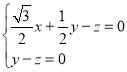得，即，令，

得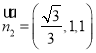

∴.

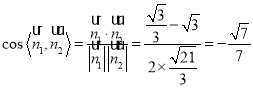所以二面角的余弦值是 .