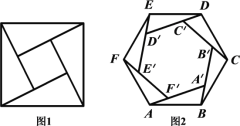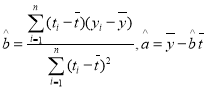题目内容
【题目】在极坐标系中,方程C:![]() 表示的曲线被称作“四叶玫瑰线”(如图)
表示的曲线被称作“四叶玫瑰线”(如图)

(1)求以极点为圆心的单位圆与四叶玫瑰线交点的极坐标和直角坐标;
(2)直角坐标系的原点与极点重合,x轴正半轴与极轴重合.求直线l:![]() 上的点M与四叶攻瑰线上的点N的距离的最小值.
上的点M与四叶攻瑰线上的点N的距离的最小值.
【答案】(1)极坐标为![]() ,直角坐标为
,直角坐标为![]() ;(2)
;(2)![]()
【解析】
(1)先求出以极点为圆心的单位圆的极坐标方程,与玫瑰线方程联立即可求出交点的极坐标;
(2)首先可得四叶玫瑰线关于直线![]() 对称,将直线方程转化为普通方程,直线
对称,将直线方程转化为普通方程,直线![]() 与直线
与直线![]() 垂直,且玫瑰线在直线
垂直,且玫瑰线在直线![]() 的同侧,即可得到距离的最小值;
的同侧,即可得到距离的最小值;
解:(1)因为![]()
![]()
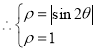
![]()
![]()
所以![]() ,
,![]()
取![]() ,得
,得![]()
从而得到单位圆与四叶玫瑰线交点的极坐标为![]() ,
,
化成直角坐标就是![]()
(2)直观发现,四叶玫瑰线关于直线![]() 对称.
对称.
事实上,将极坐标方程![]() 化作直角坐标方程得
化作直角坐标方程得![]() ,
,
将![]() 互换后方程不变,说明四叶玫瑰线关于直线
互换后方程不变,说明四叶玫瑰线关于直线![]() 对称;
对称;
将![]() 换作
换作![]() ,
,![]() 换作
换作![]() 后方程不变,说明四叶玫瑰线关于直线
后方程不变,说明四叶玫瑰线关于直线![]() 对称;
对称;
直线![]() 的普通方程是
的普通方程是![]() ,
,
直线![]() 与直线
与直线![]() 垂直,且玫瑰线在直线
垂直,且玫瑰线在直线![]() 的同侧,
的同侧,
故![]() 的最小值等于点
的最小值等于点![]() 到直线
到直线![]() 的距离:
的距离:
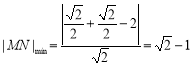 .
.

 全能测控期末小状元系列答案
全能测控期末小状元系列答案【题目】中国女排,曾经十度成为世界冠军,铸就了响彻中华的女排精神.女排精神的具体表现为:扎扎实实,勤学苦练,无所畏惧,顽强拼搏,同甘共苦,团结战斗,刻苦钻研,勇攀高峰.女排精神对各行各业的劳动者起到了激励、感召和促进作用,给予全国人民巨大的鼓舞.
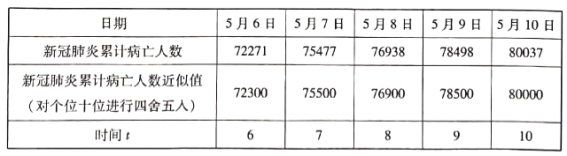
(1)看过中国女排的纪录片后,某大学掀起“学习女排精神,塑造健康体魄”的年度主题活动,一段时间后,学生的身体素质明显提高,将该大学近5个月体重超重的人数进行统计,得到如下表格:
月份x | 1 | 2 | 3 | 4 | 5 |
体重超重的人数y | 640 | 540 | 420 | 300 | 200 |
若该大学体重超重人数y与月份变量x(月份变量x依次为1,2,3,4,5…)具有线性相关关系,请预测从第几月份开始该大学体重超重的人数降至10人以下?
(2)在某次排球训练课上,球恰由A队员控制,此后排球仅在A队员、B队员和C队员三人中传递,已知每当球由A队员控制时,传给B队员的概率为![]() ,传给C队员的概率为
,传给C队员的概率为![]() ;每当球由B队员控制时,传给A队员的概率为
;每当球由B队员控制时,传给A队员的概率为![]() ,传给C队员的概率为
,传给C队员的概率为![]() ;每当球由C队员控制时,传给A队员的概率为
;每当球由C队员控制时,传给A队员的概率为![]() ,传给B队员的概率为
,传给B队员的概率为![]() .记
.记![]() ,
,![]() ,
,![]() 为经过n次传球后球分别恰由A队员、B队员、C队员控制的概率.
为经过n次传球后球分别恰由A队员、B队员、C队员控制的概率.
(i)若![]() ,B队员控制球的次数为X,求
,B队员控制球的次数为X,求![]() ;
;
(ii)若![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,证明:
,证明:![]() 为等比数列,并判断经过200次传球后A队员控制球的概率与
为等比数列,并判断经过200次传球后A队员控制球的概率与![]() 的大小.
的大小.
附1:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: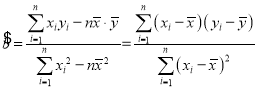 ;
;![]() .
.
附2:参考数据:![]() ,
,![]() .
.