题目内容

已知函数f（x）=x3+bx2+c．若x=-2时，f（x）有极大值0，求实数b，c的值．
考点：函数在某点取得极值的条件
专题：导数的综合应用
分析：求函数的导数，根据函数极值和导数之间的关系建立方程即可得到结论．
解答： 解：由f（x）得f'（x）=3x2+2bx，
由题意可知
f(-2)=0
f′(-2)=0
，
即
(-2)3+b×(-2)2+c=0
3×(-2)2+2b(-2)=0
，
解得
b=3
c=-4.
．
点评：本题主要考查函数极值和导数之间的关系，建立方程组是解决本题的关键．
练习册系列答案
相关题目
设集合A={2，8，a}，B={2，a2-3a+4}，且A?B，求a的值．
已知函数f（x）=cos2ωx+
3
sin2ωx（0＜ω＜1），直线x=
π
3
s是f（x）图象的一条对称轴．
（1）试求ω的值
（2）已知函数y=g（x）的图象是由y=f（x）图象上的各点的横坐标伸长到原来的2倍，然后再向左平移
2π
3
个单位长度得到，若g（2α+
π
3
）=
6
5
，α∈（0，
π
2
），求sinα的值．
求曲线f（x）=x3-x+3在点（1，f（1））处的切线方程．
经过两条异面直线a，b之外的一点P，可以作几个平面与a，b都平行？并证明你的结论．
已知圆C：x2+（y-1）2=5，直线L：mx-y+1-m=0．
①求证：对m∈R，直线L与圆C总有两个不同的交点；
②求直线L中，截圆所得的弦最长及最短时的直线方程．
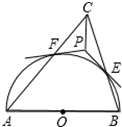如图，以锐角△ABC的边AB为直径作半圆⊙O交边BC、CA于点E、F．过点E、F分别作⊙O的切线得交点P．求证：CP⊥AB．
已知x=
1
2
(
b
a
+
a
b
)（a＞b＞0），求
2
ab
x-
x2-1
的值．
已知函数f（x）满足f（x+1）=x2+x+1，则f（x-1）=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网