题目内容
已知|
|=3,
=(1,2),
(1)若
∥
,求
的坐标;
(2)若
⊥
,求
的坐标.
| a |
| b |
(1)若
| a |
| b |
| a |
(2)若
| a |
| b |
| a |
考点:平面向量共线(平行)的坐标表示,平面向量数量积的运算
专题:平面向量及应用
分析:(1)设出向量
,由|
|=3且
∥
列方程组求解;
(2)设出向量
,由|
|=3且
⊥
列方程组求解.
| a |
| a |
| a |
| b |
(2)设出向量
| a |
| a |
| a |
| b |
解答:
解:(1)设
=x+yi,
∵|
|=3,
=(1,2),
且
∥
,
∴
,解得:
或
.
∴
=(
,
)或
=(-
,-
);
(2)由
⊥
,
∴
,解得
或
.
∴
=(-
,
)或
=(
,-
).
| a |
∵|
| a |
| b |
且
| a |
| b |
∴
|
|
|
∴
| a |
3
| ||
| 5 |
6
| ||
| 5 |
| a |
3
| ||
| 5 |
6
| ||
| 5 |
(2)由
| a |
| b |
∴
|
|
|
∴
| a |
6
| ||
| 5 |
3
| ||
| 5 |
| a |
6
| ||
| 5 |
3
| ||
| 5 |
点评:向量的平行和垂直问题是一个重要的知识点,在高考题中常常出现,常与向量的模、向量的坐标表示等联系在一起,要特别注意垂直与平行的区别.若
=(a1,a2),
=(b1,b2),则
⊥
?a1a2+b1b2=0,
∥
?a1b2-a2b1=0,是基础题.
| a |
| b |
| a |
| b |
| a |
| b |

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
A、B、C、D、E共5人站成一排,如果A、B中间隔一人,那么排法种数有( )
| A、60 | B、36 | C、48 | D、24 |
若关于x的不等式x2-4x≥m对任意x∈[0,1]恒成立,则实数m的取值范围是( )
| A、m≤-3 |
| B、m≥-3 |
| C、-3≤m≤0 |
| D、m≤-3或m≥0 |
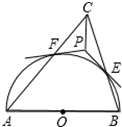 如图,以锐角△ABC的边AB为直径作半圆⊙O交边BC、CA于点E、F.过点E、F分别作⊙O的切线得交点P.求证:CP⊥AB.
如图,以锐角△ABC的边AB为直径作半圆⊙O交边BC、CA于点E、F.过点E、F分别作⊙O的切线得交点P.求证:CP⊥AB.