题目内容
已知函数f（x）=2x，则函数y=f-1（1-x）的大致图象是（ ）
A、 |
B、 |
C、 |
D、 |
考点：函数的图象
专题：函数的性质及应用
分析：根据反函数的定义先，求出y=y=log2（1-x），再根据图象的平移翻折即可得到答案
解答：
解：∵f（x）=2x，
∴f（1-x）=21-x，
∵y=f-1（1-x），
∴y=log2（1-x），
∵y=log2（1-x）的图象是由y=log2x的图象沿y轴翻折再向右平移一个单位得到的，
故选：C
∴f（1-x）=21-x，
∵y=f-1（1-x），
∴y=log2（1-x），
∵y=log2（1-x）的图象是由y=log2x的图象沿y轴翻折再向右平移一个单位得到的，
故选：C
点评：本题考查了指数函数和对数函数互为反函数，以及图象的平移和翻折，属于基础题
练习册系列答案
相关题目
已知数列{an}的通项公式为an=2n（n∈N*），现将该数列{an}的各项排列成如图的三角数阵：记M（s，t）表示该数阵中第s行的第t个数，则数阵中的偶数2010对应于（ ）| A、M（46，16） |
| B、M（46，25） |
| C、M（45，15） |
| D、M（45，25） |
已知定义在R上的函数y=f（x）满足f（x+1）=f（x-1），当-1＜x≤1时，f（x）=x3，若函数g（x）=f（x）-loga|x|恰好有6个零点，则a有取值范围是（ ）
A、a∈[
| ||||
B、a∈[0，
| ||||
C、a∈[
| ||||
D、(
|
已知i是虚数单位，复数
的虚部为（ ）
| 1-i |
| 1+i |
| A、-1 | B、1 | C、i | D、-i |
如图，在△ABC中，D是边AC上的点，且AB=AD，2AB=
BD，BC=2BD，则sinC的值为（ ）
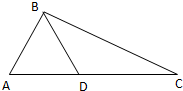
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|