题目内容
已知定义在R上的函数y=f(x)满足f(x+1)=f(x-1),当-1<x≤1时,f(x)=x3,若函数g(x)=f(x)-loga|x|恰好有6个零点,则a有取值范围是( )
A、a∈[
| ||||
B、a∈[0,
| ||||
C、a∈[
| ||||
D、(
|
考点:函数零点的判定定理
专题:函数的性质及应用
分析:本题通过典型的作图画出loga|x|以及f(x)的图象,从图象交点上交点的不同,来判断函数零点个数,从而确定底数a的大小范围
解答:
解:首先将函数g(x)=f(x)-loga|x|恰有6个零点,这个问题转化成f(x)=loga|x|的交点来解决.
数形结合:如图,f(x+1)=f(x-1),知道周期为2,当-1<x≤1时,f(x)=x3图象可以画出来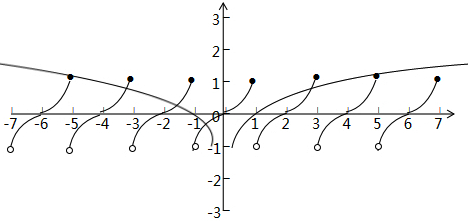 ,同理左右平移各2个单位,得到在(-7,7)上面的图象,以下分两种情况:
,同理左右平移各2个单位,得到在(-7,7)上面的图象,以下分两种情况:
(1)当a>1时,loga|x|如图所示,左侧有4个交点,右侧2个,
此时应满足loga5≤1<loga7,即loga5≤logaa<loga7,所以5≤a<7.
(2)当0<a<1时,loga|x|与f(x)交点,左侧有2个交点,右侧4个,
此时应满足loga5>-1,loga7≤-1,即loga5<-logaa≤loga7,所以5<a-1≤7.故
≤a<
综上所述,a的取值范围是:5≤a<7或
≤a<
,
故选:C.
数形结合:如图,f(x+1)=f(x-1),知道周期为2,当-1<x≤1时,f(x)=x3图象可以画出来
 ,同理左右平移各2个单位,得到在(-7,7)上面的图象,以下分两种情况:
,同理左右平移各2个单位,得到在(-7,7)上面的图象,以下分两种情况:(1)当a>1时,loga|x|如图所示,左侧有4个交点,右侧2个,
此时应满足loga5≤1<loga7,即loga5≤logaa<loga7,所以5≤a<7.
(2)当0<a<1时,loga|x|与f(x)交点,左侧有2个交点,右侧4个,
此时应满足loga5>-1,loga7≤-1,即loga5<-logaa≤loga7,所以5<a-1≤7.故
| 1 |
| 7 |
| 1 |
| 5 |
| 1 |
| 7 |
| 1 |
| 5 |
故选:C.
点评:本题考查函数零点应用转化为两个函数交点来判断,又综合了奇函数对称性对数运算等知识,属于较难的一类题,端点也要认真考虑,极容易漏掉端点

练习册系列答案
相关题目
在∠AOB的OA边上取m个点,在OB边上取n个点(均除O点外),连同O点共m+n+1个点,现任取其中三个点为顶点作三角形,可作的三角形有( )
A、
| ||||||||||||
B、
| ||||||||||||
C、
| ||||||||||||
D、
|
已知函数f(x)=2x,则函数y=f-1(1-x)的大致图象是( )
A、 |
B、 |
C、 |
D、 |
已知实数x,y满足不等式组
,则z=2x+y的最小值是( )
|
| A、2 | B、4 | C、6 | D、7 |
已知E,F,G,H是空间四点,命题甲:E,F,G,H四点不共面,命题乙:直线EF和GH不相交,则甲是乙成立的( )
| A、必要不充分条件 |
| B、充分不必要条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |