题目内容
【题目】如图,多面体![]() 中,面
中,面![]() 为矩形,面
为矩形,面![]() 面
面![]() ,
,![]() .
.
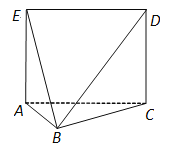
(1)求证:面![]() 面
面![]() ;
;
(2)已知多面体![]() 各顶点均在同一球面上,且该球的表面积为
各顶点均在同一球面上,且该球的表面积为![]() ,
,![]() ,当这个多面体的体积取得最大值时求其侧视图的面积.
,当这个多面体的体积取得最大值时求其侧视图的面积.
【答案】(1)见解析; (2)![]() .
.
【解析】
(1)由已知面面垂直得线面垂直,从而得线线垂直,再结合已知线线垂直得线面垂直,证得面面垂直;
(2)找出球心为![]() 与
与![]() 的交点
的交点![]() ,由球面积求出直径
,由球面积求出直径![]() 的长,得
的长,得![]() ,可得多面体的体积取得最大值时,
,可得多面体的体积取得最大值时,![]() 到
到![]() 的距离取最大值
的距离取最大值![]() ,从而易得侧视图面积.
,从而易得侧视图面积.
(1)面![]() 为矩形,面
为矩形,面![]() 面
面![]() ,
,![]() ,面
,面![]() 面
面![]()
![]() ,
,
∴![]() 平面
平面![]() ,∴
,∴![]() ,又
,又![]() ,
,![]()
∴![]() 平面
平面![]() .又
.又![]() 平面
平面![]() ,
,
∴面![]() 面
面![]() .
.
(2)设![]() 与
与![]() 交于点
交于点![]() ,
,![]() 是
是![]() 中点,连接
中点,连接![]() ,则
,则![]() ,从而
,从而![]() 平面
平面![]() 主,
主,![]() 是
是![]() 外心,∴
外心,∴![]() 是多面体
是多面体![]() 中外接球球心,
中外接球球心,
由![]() ,得
,得![]() ,又
,又![]() ,
,
∴![]() .又
.又![]() ,
,![]() 为直角三角形,
为直角三角形,
∴当![]() 斜边
斜边![]() 上的高等于
上的高等于![]() 时,体积取得最大值.
时,体积取得最大值.
此时其侧视图也为直角三角形,面积为![]() .
.


练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目