题目内容
9.若F1、F2是椭圆$\frac{x^2}{16}$+$\frac{y^2}{9}$=1的两个焦点,过F1作直线与椭圆交于A、B,则△ABF2的周长为16.分析 根据题意,分析可得△ABF2的周长等于AF1+AF2+BF1+BF2=4a,由椭圆的标准方程可得a的值,计算可得答案.
解答 解:根据题意,在椭圆$\frac{x^2}{16}$+$\frac{y^2}{9}$=1中,a=4,则
${l}_{△AB{F}_{2}}$=AB+AF2+BF2=AF1+BF1+AF2+BF2=AF1+AF2+BF1+BF2=4a=8,
即△ABF2的周长为8;
故答案为16.
点评 本题考查椭圆的性质,注意将△ABF2的周长转化为A、B两点到椭圆两个焦点的距离之和.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
18.曲线f(x)=-x3+3x2在点(1,f(1))处的切线截圆x2+(y+1)2=4所得弦长为( )
| A. | 4 | B. | 2$\sqrt{2}$ | C. | 2 | D. | $\sqrt{2}$ |
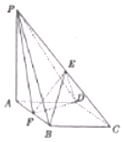 如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°,AB=2,PA=3,PA⊥底面ABCD,E,F分别是PC,AB的中点.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°,AB=2,PA=3,PA⊥底面ABCD,E,F分别是PC,AB的中点.