题目内容
1.已经集合A={x|(8x-1)(x-1)≤0};集合C={x|a<x<2a+5}(1)若${(\frac{1}{4})^t}∈A$,求实数t的取值集合B;
(2)在(1)的条件下,若(A∪B)⊆C,求实数a的取值范围.
分析 (1)求出集合A的等价条件,结合指数不等式的性质进行求解即可.
(2)根据集合的基本运算以及集合关系建立不等式关系进行求解即可.
解答 解:由已知集合A={x|(8x-1)(x-1)≤0}={x|$\frac{1}{8}$≤x≤1}…(2分)
(1)若${(\frac{1}{4})^t}∈A$,即|$\frac{1}{8}$≤($\frac{1}{4}$)t≤1,即2-3≤2-2t≤20…(4分)
则-3≤-2t≤0,
即0≤t≤$\frac{3}{2}$,故集合B=[0,$\frac{3}{2}$]…(6分)
(2)在(1)的条件下,A∪B=[0,$\frac{3}{2}$]…(8分)
由(A∪B)⊆C,即[0,$\frac{3}{2}$]⊆(a,2a+5),
∴$\left\{\begin{array}{l}{a≤0}\\{2a+5≥\frac{3}{2}}\end{array}\right.$,…(11分)
解得:-$\frac{7}{4}$≤a≤0…(12分)
点评 本题主要考查集合的基本运算以及集合关系的应用,根据不等式的性质求出 集合的等价条件是解决本题的关键.

练习册系列答案
相关题目
16.已知点A(1,-3),B(-5,5),则线段AB中点到直线4x-3y+1=0的距离等于( )
| A. | $\frac{4}{5}$ | B. | $\frac{10}{7}$ | C. | $\frac{12}{5}$ | D. | 2 |
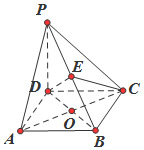 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,四边形ABCD是菱形,AC=2,BD=2$\sqrt{3}$,且AC,BD交于点O,E是PB上任意一点.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,四边形ABCD是菱形,AC=2,BD=2$\sqrt{3}$,且AC,BD交于点O,E是PB上任意一点. 已知MOD函数是一个求余函数,其格式为MOD(n,m),其结果为n除以m的余数,例如MOD(12,5)=2,下面是一个算法的程序框图,当输入的n为77时,则输出的结果为( )
已知MOD函数是一个求余函数,其格式为MOD(n,m),其结果为n除以m的余数,例如MOD(12,5)=2,下面是一个算法的程序框图,当输入的n为77时,则输出的结果为( )