题目内容
| 2n2-2n+83 |
| 2n+1 |
考点:基本不等式
专题:不等式的解法及应用
分析:变形可得原式
•[(2n+1)+
-4],由基本不等式可得.
| 1 |
| 2 |
| 169 |
| 2n+1 |
解答:
解:原式=
•
=
•
=
•[(2n+1)+
-4]≥
•[2
-4]=11
当且仅当(2n+1)=
即n=6时取等号,
故答案为:11
| 1 |
| 2 |
| 4n2-4n+166 |
| 2n+1 |
| 1 |
| 2 |
| (2n+1)2-4(2n+1)+169 |
| 2n+1 |
=
| 1 |
| 2 |
| 169 |
| 2n+1 |
| 1 |
| 2 |
(2n+1)
|
当且仅当(2n+1)=
| 169 |
| 2n+1 |
故答案为:11
点评:本题考查基本不等式,凑出可利用基本不等式的形式是解决问题的关键,属中档题.

练习册系列答案
相关题目
方程
=
表示的曲线是( )
| 1+|x| |
| 1-y |
| A、两条线段 |
| B、两条直线 |
| C、两条射线 |
| D、一条射线和一条线段 |
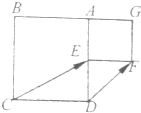 如图,已知正方形ABCD的边长为2,点E为边AD的中点,以AE为边向外作正方形AEFG,现将正方形AEFG绕点A按顺时针方向转动至AE与AB重合,则
如图,已知正方形ABCD的边长为2,点E为边AD的中点,以AE为边向外作正方形AEFG,现将正方形AEFG绕点A按顺时针方向转动至AE与AB重合,则