题目内容
一次函数f(x)是R上的增函数,已知f[f(x)]=16x+5
(1)求函数f(x)的解析式;
(2)若函数g(x)=f(x)(x+1),求函数g(x)在区间[-1,1]上的最大值和最小值.
(1)求函数f(x)的解析式;
(2)若函数g(x)=f(x)(x+1),求函数g(x)在区间[-1,1]上的最大值和最小值.
考点:函数解析式的求解及常用方法,函数的最值及其几何意义
专题:待定系数法,函数的性质及应用
分析:(1)设出一次函数f(x)的解析式,利用f[f(x)]=16x+5,求出f(x)的解析式;
(2)求出函数g(x)=f(x)(x+1),再求g(x)在区间[-1,1]上的最值即可.
(2)求出函数g(x)=f(x)(x+1),再求g(x)在区间[-1,1]上的最值即可.
解答:
解:(1)设f(x)=kx+b(k>0),
∴f[f(x)]=k(kx+b)+b
=k2x+kb+b
=16x+5,
∴
;
解得k=4,b=1;
∴f(x)=4x+1;
(2)∵函数g(x)=f(x)(x+1)
=(4x+1)(x+1)
=4x2+5x+1,
∴当x=-
=-
时,
g(x)取得最小值是g(x)min=g(-
)=-
;
当x=1时,g(x)取得最大值是g(x)max=g(1)=10;
∴函数g(x)在区间[-1,1]上的最大值是10,最小值是-
.
∴f[f(x)]=k(kx+b)+b
=k2x+kb+b
=16x+5,
∴
|
解得k=4,b=1;
∴f(x)=4x+1;
(2)∵函数g(x)=f(x)(x+1)
=(4x+1)(x+1)
=4x2+5x+1,
∴当x=-
| 5 |
| 2×4 |
| 5 |
| 8 |
g(x)取得最小值是g(x)min=g(-
| 5 |
| 8 |
| 9 |
| 16 |
当x=1时,g(x)取得最大值是g(x)max=g(1)=10;
∴函数g(x)在区间[-1,1]上的最大值是10,最小值是-
| 9 |
| 16 |
点评:本题考查了用待定系数法求函数解析式的应用问题,也考查了一次函数与二次函数的图象与性质的应用问题,是基础题目.

练习册系列答案
相关题目
如果点P在平面区域
上,点Q在曲线x2+(y+2)2=1上,那么|PQ|的最大值为( )
|
| A、5 | ||||
B、
| ||||
C、2
| ||||
D、
|
不等式组
的解集是( )
|
| A、{x|x<-2} |
| B、{x|x>1} |
| C、{x|-2<x<1} |
| D、∅ |
过点M(-1,2)和N(2,-1)的直线的倾斜角是( )
| A、135° | B、45° |
| C、45°或135° | D、-45° |
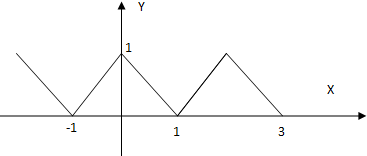
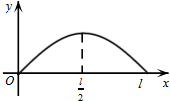 点P从O点出发,按逆时针方向沿周长为l的图形运动一周,O、P两点间的距离y与点P所走路程x的函数关系如图,那么点P所走的图形是( )
点P从O点出发,按逆时针方向沿周长为l的图形运动一周,O、P两点间的距离y与点P所走路程x的函数关系如图,那么点P所走的图形是( )