题目内容
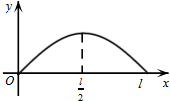 点P从O点出发,按逆时针方向沿周长为l的图形运动一周,O、P两点间的距离y与点P所走路程x的函数关系如图,那么点P所走的图形是( )
点P从O点出发,按逆时针方向沿周长为l的图形运动一周,O、P两点间的距离y与点P所走路程x的函数关系如图,那么点P所走的图形是( )A、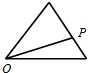 |
B、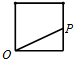 |
C、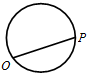 |
D、 |
考点:函数的图象
专题:函数的性质及应用
分析:认真观察函数的图象,根据其运动特点,采用排除法求解.
解答:
解:观察函数的运动图象,可以发现两个显著特点:
①点P运动到周长的一半时,OP最大;
②点P的运动图象是抛物线.
设点M为周长的一半,如下图所示:
由图可知,

图1中,OM≤OP,不符合条件①,因此排除选项A;
图4中,OM≤OP,不符合条件①,因此排除选项D.
另外,在图2中,当点P在线段OA上运动时,y=x,其图象是一条线段,不符合条件②,因此排除选项B.
故选:C.
①点P运动到周长的一半时,OP最大;
②点P的运动图象是抛物线.
设点M为周长的一半,如下图所示:
由图可知,

图1中,OM≤OP,不符合条件①,因此排除选项A;
图4中,OM≤OP,不符合条件①,因此排除选项D.
另外,在图2中,当点P在线段OA上运动时,y=x,其图象是一条线段,不符合条件②,因此排除选项B.
故选:C.
点评:本题考查动点问题的函数图象,考查对于运动问题的深刻理解,解题关键是认真分析函数图象的特点.选项D中出现了椭圆,增加了试题的难度.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若a=30.2,b=logπ3,c=log3cos
π,则( )
| ||
| 4 |
| A、b>c>a |
| B、b>a>c |
| C、a>b>c |
| D、c>a>b |
集合A={x|{y=
},B={y|y=x2-2x},求A∩B=( )
| x2-4 |
| A、[-1,+∞) |
| B、[2,+∞) |
| C、(-∞,-2]∪[2,+∞) |
| D、(-∞,-2]∪[-1,+∞) |
 某程序的框图如图所示,执行该程序,若输入的p为l6,则输出的n的值为
某程序的框图如图所示,执行该程序,若输入的p为l6,则输出的n的值为