题目内容
15.设不等式组$\left\{\begin{array}{l}x+y≥0\\ x≤2\\ y≤0\end{array}\right.$表示的平面区域为D,在区域D内随机取一个点,则此点到坐标原点的距离大于2的概率是1-$\frac{π}{4}$.分析 作出不等式组对应的平面区域,求出对应的面积,结合几何概型的概率公式进行计算即可.
解答  解:作出不等式组对应的平面区域如图,
解:作出不等式组对应的平面区域如图,
对应区域为三角形OAB,A(2,0),B(2,-2),
则三角形OAB的面积S=$\frac{1}{2}×2×2$=2,
∠AOB=45°,
则扇形OAC的面积S=$\frac{45}{360}×π×{2}^{2}$=$\frac{π}{2}$,
则圆外的面积S=2-$\frac{π}{2}$,
则点到坐标原点的距离大于2的概率P=$\frac{2-\frac{π}{2}}{2}$=1-$\frac{π}{4}$,
故答案为:1-$\frac{π}{4}$
点评 本题给出不等式组表示的平面区域,求在区域内投点使该到原点距离大于2的概率,着重考查了二元一次不等式组表示的平面区域和几何概型等知识点,属于基础题.

练习册系列答案
相关题目
20.已知棱长为$\sqrt{3}$的正方体ABCD-A1B1C1D1内部有一圆柱,此圆柱恰好以直线AC1为轴,则该圆柱侧面积的最大值为( )
| A. | $\frac{{9\sqrt{2}}}{8}π$ | B. | $\frac{{9\sqrt{2}}}{4}π$ | C. | $2\sqrt{3}π$ | D. | $3\sqrt{2}π$ |
5.将函数y=$\sqrt{3}cosx+sinx({x∈R})$的图象向左平移m(m>0)个单位长度后,所得到的图象关于y轴对称,则m的最小值是( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{12}$ | C. | $\frac{π}{3}$ | D. | $\frac{5π}{6}$ |
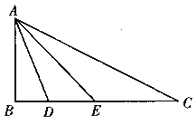 如图,在△ABC中,∠B=90°,∠BAD=∠DAE=∠EAC,BD=2,DE=3.
如图,在△ABC中,∠B=90°,∠BAD=∠DAE=∠EAC,BD=2,DE=3.