Question

17．某蔬菜基地种植甲、乙两种无公害蔬菜，生产一吨甲菜需用电力9千瓦时，耗肥4吨，3个工时；生产一吨乙菜需用电力5千瓦时，耗肥5吨，10个工时；现该基地有电力360千瓦时，肥200吨，300个工时，已知生产一吨甲菜获利700元，已知生产一吨乙菜获利1200元，在上述条件限制下，问如何甲、乙两种蔬菜的种植，才能使利润最大？试写出这个问题的约束条件和目标函数．

Answer 1

分析 由题意设甲、乙两种蔬菜各种植x吨，y吨，利润为z元，从而写出约束条件及目标函数；从而利用线性规划求解即可．

解答 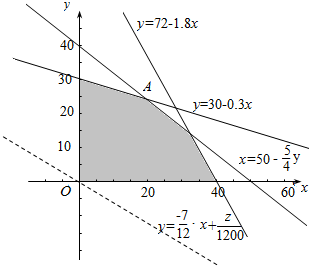解：由题意，设甲、乙两种蔬菜各种植x吨，y吨，利润为z元，
则约束条件如下，
$\left\{\begin{array}{l}{9x+5y≤360}\\{4x+5y≤200}\\{3x+10y≤300}\\{x≥0}\\{y≥0}\end{array}\right.$；
目标函数z=700x+1200y；
作平面区域如图，
化目标函数z=700x+1200y为y=-$\frac{7}{12}$x+$\frac{z}{1200}$；
联立方程$\left\{\begin{array}{l}{3x+10y=300}\\{4x+5y=200}\end{array}\right.$，
解得，x=20，y=24；
此时目标函数z=700x+1200y有最大值700×20+1200×24=42800（元）；
即甲、乙两种蔬菜各种植20吨，24吨时，利润有最大值为42800元．

点评 本题考查了线性规划在实际问题中的应用．