题目内容
若数列{n(n+4)(
)n}中的最大项是第k项,则k=( )
| 2 |
| 3 |
| A、4 | B、5 | C、6 | D、7 |
考点:数列的函数特性
专题:点列、递归数列与数学归纳法
分析:求数列的最大值,只要解不等式
,即可得到结论.
|
解答:
解:若第k项最大,k∈N,且k≥1,则
,
即
,
即
,
∴
,
∵k>0,
∴
≤k≤1+
∵k是整数,
∴k=4,即a4最大
故选:A.
|
即
|
即
|
∴
|
∵k>0,
∴
| 10 |
| 10 |
∵k是整数,
∴k=4,即a4最大
故选:A.
点评:本题考查数列的最值问题,利用不等式的性质解不等式即可得到结论.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
线性回归方程表示的直线
=a+bx,必定过( )
 |
| y |
| A、(0,0)点 | ||||
B、(
| ||||
C、(0,
| ||||
D、(
|
从装有2个红球和2个黒球的口袋内任取2个球,下面属于互斥而不对立的两个事件是( )
| A、至少有一个黒球与都是红球 |
| B、至少有一个黒球与都是黒球 |
| C、至少有一个黒球与恰有1个红球 |
| D、恰有2个黒球与恰有2个红球 |
炼钢时钢水的含碳量与冶炼时间有( )
| A、确定性关系 | B、相关关系 |
| C、函数关系 | D、无任何关系 |
直线x+y=0与圆(x-2)2+y2=4相交所得线段的长度为( )
A、
| ||||
B、
| ||||
| C、2 | ||||
D、2
|
在△ABC中,角A、B、C所对的边分别为a、b、c,若acosB+bcosA=csinC且a=b,则角B等于( )
| A、30° | B、45° |
| C、60° | D、90° |



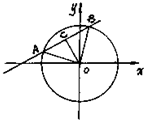 已知直线:y=k(x+2)与圆O:x2+y2=4相交于A、B两点,O是坐标原点,三角形ABO的面积为S.
已知直线:y=k(x+2)与圆O:x2+y2=4相交于A、B两点,O是坐标原点,三角形ABO的面积为S.