题目内容
在△ABC中，已知cosA=
，cos（A-B）=
，且B＜A．
（1）求角B和sinC的值；
（2）若△ABC的边AB=5，求边AC的长．
| 1 |
| 7 |
| 13 |
| 14 |
（1）求角B和sinC的值；
（2）若△ABC的边AB=5，求边AC的长．
考点：正弦定理,同角三角函数基本关系的运用
专题：计算题,三角函数的求值
分析：（1）利用已知条件和同角三角函数关系求得sinA和sin（A-B）的值，进而求得cosB的值，求得B，利用C和A+B互补，利用两角和公式求得sinC的值．
（2）利用正弦定理和已知条件求得AC．
（2）利用正弦定理和已知条件求得AC．
解答：
解：（1）∵cosA=
＞0，cos(A-B)=
＞0，
∴0＜A＜
，0＜A-B＜
∴sinA=
=
=
，sin（A-B）=
=
=
，
∴cosB=cos[A-（A-B）]=cosAcos（A-B）+sinAsin（A-B）=
•
+
•
=
，
∵0＜B＜π
∴B=
．
∵在△ABC中，C=π-（A+B）
∴sinC=sin[π-（A+B）]=sin（A+B）=sinAcosB+cosAsinB=
×
+
×
=
．
（2）在△ABC中，由正弦定理得：
=
，
∴AC=
=
=7．
| 1 |
| 7 |
| 13 |
| 14 |
∴0＜A＜
| π |
| 2 |
| π |
| 2 |
∴sinA=
| 1-cos2A |
1-(
|
4
| ||
| 7 |
| 1-cos2(A-B) |
1-(
|
3
| ||
| 14 |
∴cosB=cos[A-（A-B）]=cosAcos（A-B）+sinAsin（A-B）=
| 1 |
| 7 |
| 13 |
| 14 |
4
| ||
| 7 |
3
| ||
| 14 |
| 1 |
| 2 |
∵0＜B＜π
∴B=
| π |
| 3 |
∵在△ABC中，C=π-（A+B）
∴sinC=sin[π-（A+B）]=sin（A+B）=sinAcosB+cosAsinB=
4
| ||
| 7 |
| 1 |
| 2 |
| 1 |
| 7 |
| ||
| 2 |
5
| ||
| 14 |
（2）在△ABC中，由正弦定理得：
| AB |
| sinC |
| AC |
| sinB |
∴AC=
| AB•sinB |
| sinC |
5×
| ||||
|
点评：本题主要考查正弦定理的运用．解题过程巧妙的利用了互补关系构造出关系式，利用两角和公式求得答案．
练习册系列答案
相关题目
炼钢时钢水的含碳量与冶炼时间有（ ）
| A、确定性关系 | B、相关关系 |
| C、函数关系 | D、无任何关系 |
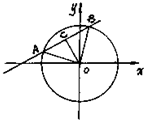已知直线：y=k（x+2）与圆O：x2+y2=4相交于A、B两点，O是坐标原点，三角形ABO的面积为S．