题目内容
1. 如图,四棱锥P-ABCD中,底面ABCD是正方形,PA是四棱锥P-ABCD的高,PA=AB=2,点M,N,E分别是PD,AD,CD的中点.
如图,四棱锥P-ABCD中,底面ABCD是正方形,PA是四棱锥P-ABCD的高,PA=AB=2,点M,N,E分别是PD,AD,CD的中点.(1)求证:平面MNE∥平面ACP;
(2)求四面体AMBC的体积.
分析 (1)由点M,N,E分别是PD,AD,CD的中点,得MN∥PA,NE∥AC,由此能证明平面MNE∥平面ACP.
(2)由已知得MN⊥平面ABC,且MN=$\frac{1}{2}PA=1$,由此能求出四面体AMBC的体积.
解答 证明:(1)∵点M,N,E分别是PD,AD,CD的中点,
∴MN∥PA,NE∥AC,
PA∩AC=A,MN∩NE=N,
PA,AC?平面PAC,MN,NE?平面MNE,
∴平面MNE∥平面ACP.
解:(2)∵四棱锥P-ABCD中,底面ABCD是正方形,PA是四棱锥P-ABCD的高,
PA=AB=2,点M,N,E分别是PD,AD,CD的中点.
∴MN⊥平面ABC,且MN=$\frac{1}{2}PA=1$,
${S}_{△ABC}=\frac{1}{2}×2×2$=2,
∴四面体AMBC的体积V=$\frac{1}{3}×{S}_{△ABC}×MN$=$\frac{1}{3}×2×1$=$\frac{2}{3}$.
点评 本题考查面面平行的证明,考查四面体的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
16.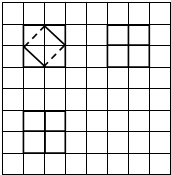 如图所示,网格纸上小正方形的边长为1,粗实线及粗虚线画出的是某多面体的三视图,则该多面体的体积为( )
如图所示,网格纸上小正方形的边长为1,粗实线及粗虚线画出的是某多面体的三视图,则该多面体的体积为( )
 如图所示,网格纸上小正方形的边长为1,粗实线及粗虚线画出的是某多面体的三视图,则该多面体的体积为( )
如图所示,网格纸上小正方形的边长为1,粗实线及粗虚线画出的是某多面体的三视图,则该多面体的体积为( )| A. | 6 | B. | $\frac{20}{3}$ | C. | 7 | D. | $\frac{22}{3}$ |
13.从个位数与十位数之和为偶数的两位数中任取一个,其中个位数为2或3的概率为( )
| A. | $\frac{5}{9}$ | B. | $\frac{1}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{4}{9}$ |