题目内容
15．
某高中体育小组共有男生24人，其50m跑成绩记作ai（i=1，2，…，24），若成绩小于6.8s为达标，则如图所示的程序框图的功能是（ ）| A． | 求24名男生的达标率 | B． | 求24名男生的不达标率 | ||
| C． | 求24名男生的达标人数 | D． | 求24名男生的不达标人数 |
分析 由题意，从成绩中搜索出大于6.8s的成绩，计算24名中不达标率．
解答 解：由题意可知，k记录的是时间超过6.8s的人数，而i记录是的参与测试的人数，因此$\frac{k}{i}$表示不达标率；
故选B．
点评 本题考查程序框图的理解以及算法功能的描述．
练习册系列答案
相关题目
5．把函数f（x）=2sin（x+2φ）（|φ|＜$\frac{π}{2}$）的图象向左平移$\frac{π}{2}$个单位长度之后，所得图象关于直线$x=\frac{π}{4}$对称，且f（0）＜f（$\frac{π}{2}$-φ），则φ=（ ）
| A． | $\frac{π}{8}$ | B． | $\frac{3π}{8}$ | C． | $-\frac{π}{8}$ | D． | $-\frac{3π}{8}$ |
6．
如图，A1，A2为椭圆$\frac{x^2}{9}+\frac{y^2}{5}=1$长轴的左、右端点，O为坐标原点，S，Q，T为椭圆上不同于A1，A2的三点，直线QA1，QA2，OS，OT围成一个平行四边形OPQR，则|OS|2+|OT|2=（ ）
如图，A1，A2为椭圆$\frac{x^2}{9}+\frac{y^2}{5}=1$长轴的左、右端点，O为坐标原点，S，Q，T为椭圆上不同于A1，A2的三点，直线QA1，QA2，OS，OT围成一个平行四边形OPQR，则|OS|2+|OT|2=（ ）| A． | 14 | B． | 12 | C． | 9 | D． | 7 |
3．正方形ABCD与等边三角形BCE有公共边BC，若∠ABE=120°，则BE与平面ABCD所成角的大小为（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{3}$ | C． | $\frac{π}{4}$ | D． | $\frac{π}{2}$ |
如图，在平面直角坐标系xOy中，椭圆Ω：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\;（a＞b＞0）$的离心率为$\frac{{\sqrt{2}}}{2}$，直线l：y=2上的点和椭圆Ω上的点的距离的最小值为1．
7．已知集合A={x|x2-2x-3＜0}，B={x||x|＜2}，则A∩B=（ ）
| A． | {x|-2＜x＜2} | B． | {x|-2＜x＜3} | C． | {x|-1＜x＜3} | D． | {x|-1＜x＜2} |
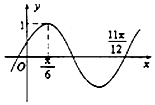已知函数f（x）=sinωx（ω＞0），若函数y=f（x+a）（a＞0）的部分图象如图所示，则ω=2，a的最小值是$\frac{π}{12}$．