题目内容
给出下列三个结论:
①当a为任意实数时,直线(a+1)x-y+2a+1=0恒过下点P,则P在圆x2+y2=5上;
②抛物线y=4x2的焦点坐标是(0,1);
③双曲线x2-
=1的离心率e=2.
其中所有的正确的结论是( )
①当a为任意实数时,直线(a+1)x-y+2a+1=0恒过下点P,则P在圆x2+y2=5上;
②抛物线y=4x2的焦点坐标是(0,1);
③双曲线x2-
| y2 |
| 3 |
其中所有的正确的结论是( )
| A、①② | B、②③ | C、①③ | D、①②③ |
考点:命题的真假判断与应用
专题:直线与圆,圆锥曲线的定义、性质与方程
分析:①,易求直线(a+1)x-y+2a+1=0恒过定点点P(-2,-1),显然点P在圆x2+y2=5上,可判断①;
②,抛物线y=4x2的焦点坐标是(0,
),可判断②;
③,易求双曲线x2-
=1的离心率e=2,可判断③.
②,抛物线y=4x2的焦点坐标是(0,
| 1 |
| 16 |
③,易求双曲线x2-
| y2 |
| 3 |
解答:
解:对于①,∵(a+1)x-y+2a+1=0?(x+2)a+(x-y+1)=0,由
得:
,
∴直线(a+1)x-y+2a+1=0恒过定点P(-2,-1),显然点P在圆x2+y2=5上,故①正确;
对于②,抛物线y=4x2中,其标准方程为:x2=
y,其焦点坐标是(0,
),故②错误;
对于③,双曲线x2-
=1的离心率e=
=2,故③正确.
综上所述,所有的正确的结论是①③,
故选:C.
|
|
∴直线(a+1)x-y+2a+1=0恒过定点P(-2,-1),显然点P在圆x2+y2=5上,故①正确;
对于②,抛物线y=4x2中,其标准方程为:x2=
| 1 |
| 4 |
| 1 |
| 16 |
对于③,双曲线x2-
| y2 |
| 3 |
| ||
| 1 |
综上所述,所有的正确的结论是①③,
故选:C.
点评:本题考查命题的判断与应用,着重考查直线恒过定点、抛物线与双曲线的几何性质的应用,属于中档题.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
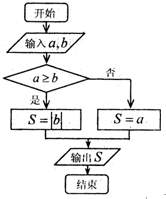 定义某种运算?,a?b的运算原理如图所示:设f(x)=(0?x)x,则f(x)在区间[-2,2]上的最小值为( )
定义某种运算?,a?b的运算原理如图所示:设f(x)=(0?x)x,则f(x)在区间[-2,2]上的最小值为( )| A、-2 | B、-4 | C、2 | D、-8 |
已知函数f(x)=
满足对任意x1≠x2,都有
>0 成立,则a的取值范围是( )
|
| f(x1)-f(x2) |
| x1-x2 |
| A、(1,2] | ||
| B、(1,2) | ||
C、(
| ||
D、[
|
下列函数既是定义域上的减函数又是奇函数的是( )
| A、f(x)=|x| | ||
B、f(x)=
| ||
| C、f(x)=-x3 | ||
| D、f(x)=x|x| |
已知i是虚数单位,m和n都是实数,且m(1+i)=11+ni,则(
)2014=( )
| m+ni |
| m-ni |
| A、i | B、-i |
| C、1 | D、n∈N* |