题目内容
2.二次函数f(x)=x2-2x+2,x∈[-5,5].最小值是1,最大值是37.分析 先对已知函数进行配方,求对称轴,结合函数的单调性,即对称轴和区间的位置关系,可求函数的最大值与最小值.
解答 解:f(x)=x2-2x+2=(x-1)2+1,
∵x∈[,-5,5]
∴f(x)=(x-1)2+1在[-5,1]上单调递减,在[1,5]上单调递增
当x=1时,函数有最小值f(1)=1
∵开口向上的抛物线离对称轴越远,函数值越大,
当x=-5时,函数有最大值f(-5)=37,
故答案为:1,37.
点评 本题考查了二次函数在闭区间上的最值问题,开口向上的二次函数离对称轴越远函数值越大,开口向下的二次函数离对称轴越近函数值越小.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
13.下列命题中,真命题是( )
| A. | 存在x∈R,使得ex≤0 | B. | 任意x∈R,2x>x2 | ||
| C. | a>1,b>1是ab>1的必要条件 | D. | x2+$\frac{2}{x}$≥3对任意正实数x恒成立 |
10.函数f(x)=$\frac{\root{3}{x-4}}{a{x}^{2}+4ax+3}$的定义域为R,那么实数a的取值范围是( )
| A. | [0.$\frac{3}{4}$) | B. | (0,$\frac{3}{4}$) | C. | (-$\frac{3}{4}$,+∞) | D. | (-∞,+∞) |
17.如图所示的程序框图,运行后输出结果为( )
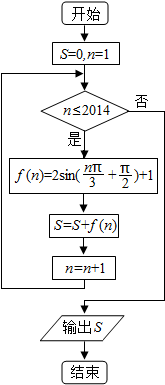

| A. | 2017 | B. | 4028 | C. | 2014 | D. | 2011 |
7.已知数列{an}的前n项和Sn=2n(n∈N*),则n≥2时,a12+a22+…+an2=( )
| A. | $\frac{1}{3}({4^n}-1)$ | B. | $\frac{1}{3}({4^n}+8)$ | C. | $\frac{1}{3}{({2^n}-1)^2}$ | D. | $\frac{1}{3}{({2^n}+4)^2}$ |
12.已知|$\overrightarrow{OA}$|=$\sqrt{3}$,$\overrightarrow{OA}$•$\overrightarrow{OB}$=0,则$\overrightarrow{OA}$•$\overrightarrow{AB}$等于( )
| A. | -3 | B. | 3 | C. | -$\frac{1}{3}$ | D. | $\frac{1}{3}$ |