题目内容
11．设n为整数，如果点（5，n）在两平行线6x-8y+1=0和3x-4y+5=0之间，则m=4或5．分析 根据题意可得-10≤6×5-8n≤-1，由此求得n的范围，再结合n为整数，求得n的值．
解答 解：∵夹在两平行线6x-8y+1=0和6x-8y+10=0之间所有点满足-10≤6x+8y≤-1，
而点（5，n）在两平行线6x-8y+1=0和3x-4y+5=0之间，
∴-10≤6×5-8n≤-1，求得$\frac{31}{8}$≤n≤5，故整数n=4或5，
故答案为：4或5．
点评 本题主要考查两条平行线间的距离公式，属于基础题．
练习册系列答案
相关题目
1．若复数z=$\frac{1-2i}{i}$的共轭复数是$\overline{z}$=a+bi（a，b∈R），其中i为虚数单位，则点（a，b）为（ ）
| A． | （-1.2） | B． | （-2，1） | C． | （1，-2） | D． | （2，-1） |
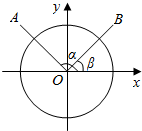如图，以ox为始边作角α与β（0＜β＜α＜π），它们的终边 分别与单位圆相交于点A、B．已知点A的坐标为（-$\frac{3}{5}$，$\frac{4}{5}$）．
2015年我国将加快阶梯水价的推行，原则是“保基本、建机制、促节约”，其中“保基本是指保证至少80%的居民用户用水价格不变，为响应国家政策，制定合理的阶梯用水价格，某城市采用简单随机抽样的方法分别从郊区和城区抽取5户和20户居民的年人均用水量进行调研，抽取的数据的茎叶图如图（单位：吨）．