题目内容
已知在等差数列{an}中，a1=
，a9+a10=0．
（1）求数列{an}的通项公式；
（2）求|a1|+|a2|+|a3|+…+|a18|的值．
| 17 |
| 2 |
（1）求数列{an}的通项公式；
（2）求|a1|+|a2|+|a3|+…+|a18|的值．
考点：数列的求和,等差数列的通项公式
专题：等差数列与等比数列
分析：（1）利用等差数列的性质，联立方程组解得公差d，即可得出结论；
（2）去掉绝对值，有等差数列的性质及前n项和公式，求得即可．
（2）去掉绝对值，有等差数列的性质及前n项和公式，求得即可．
解答：
解：（1）∵a1=
，a9+a10=0，
∴（a1+8d）+（a1+9d）=0，
即2a1+17d=0，
∴d=-1，
∴an=
-（n-1），即an=
-n．
（2）∵a1=
，a9+a10=0，
∴a9＞0，a10＜0，
∴|a1|+|a2|+|a3|+…+|a18|=（a1+a2+…+a9）-（a10+a11+…+a18）
=2 （ a1+a2+…+a9 ）-（ a1+a2+…+a9+a10+a11+…+a18）
=2 （ a1+a2+…+a9 ）=2•[9a1+
•(-1)]=81．
| 17 |
| 2 |
∴（a1+8d）+（a1+9d）=0，
即2a1+17d=0，
∴d=-1，
∴an=
| 17 |
| 2 |
| 19 |
| 2 |
（2）∵a1=
| 17 |
| 2 |
∴a9＞0，a10＜0，
∴|a1|+|a2|+|a3|+…+|a18|=（a1+a2+…+a9）-（a10+a11+…+a18）
=2 （ a1+a2+…+a9 ）-（ a1+a2+…+a9+a10+a11+…+a18）
=2 （ a1+a2+…+a9 ）=2•[9a1+
| 9(9-1) |
| 2 |
点评：本题主要考查等差数列的定义，通项公式及前n项和公式的运用，考查学生的方程思想的运用及运算求解能力，属中档题．
练习册系列答案
口算能手系列答案
相关题目
设
，
为单位向量．且
，
的夹角为
，若
=x
+（1-x）
，x∈[0，1]，
=2
则向量
在
方向上的投影的取值范围是（ ）
| e1 |
| e2 |
| e1 |
| e2 |
| π |
| 3 |
| a |
| e1 |
| e2 |
| b |
| e1 |
| a |
| b |
A、[
| ||
| B、[0，2] | ||
| C、[0，1] | ||
| D、[1，3] |
如图所示的程序是用来（ ）
| A、计算3×10的值 |
| B、计算39值 |
| C、计算310的值 |
| D、计算1×2×3×…×10的值 |
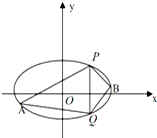已知椭圆C方程为