题目内容
实数x,y满足等式(x+3)2+(y+2)2=4,则w=
的取值范围是 .
| y-1 |
| x+1 |
考点:直线与圆的位置关系
专题:直线与圆
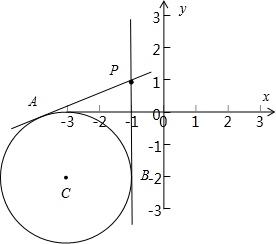
分析:所求表达式转化为直线方程,表示经过点P(-1,1)的直线,w为直线的斜率,题目等价于求同时经过点P(-1,1)和圆上的点的直线中斜率的最大最小值,当过P直线与圆相切时,如图所示,直线PA与直线PB与圆相切,此时直线PB斜率不存在,利用点到直线的距离公式表示出圆心C到直线PA的距离d,令d=r求出此时k的值,确定出w的范围,即为所求式子的范围.
解答:
 解:w=
解:w=
,则y=wx+(w+1)表示经过点P(-1,1)的直线,w为直线的斜率,
∴求w的取值范围就等价于求同时经过点P(-1,1)和圆上的点的直线中斜率的最大最小值,
从图中可知,当过P的直线与圆相切时斜率取最大最小值,此时对应的直线斜率分别为kPB和kPA,
由圆心C(-3,-2)到直线y=wx+(w+1)的距离
=2,
解得:w=
,kPA=
,kPB不存在,则w的取值范围是[
,+∞).
故答案为:[
,+∞).
 解:w=
解:w=| y-1 |
| x+1 |
∴求w的取值范围就等价于求同时经过点P(-1,1)和圆上的点的直线中斜率的最大最小值,
从图中可知,当过P的直线与圆相切时斜率取最大最小值,此时对应的直线斜率分别为kPB和kPA,
由圆心C(-3,-2)到直线y=wx+(w+1)的距离
| |-3w+2+w+1| | ||
|
解得:w=
| 5 |
| 12 |
| 5 |
| 12 |
| 5 |
| 12 |
故答案为:[
| 5 |
| 12 |
点评:此题考查了直线与圆的位置关系,直线与圆的位置关系由d与r来判断:当d>r时,直线与圆相离;当d=r时,直线与圆相切;当d<r时,直线与圆相交(d为圆心到直线的距离,r为圆的半径).熟练掌握数形结合思想是解本题的关键.

练习册系列答案
相关题目
已知i为虚数单位,a∈R,若(a-1)(a+1+i)是纯虚数,则a的值为( )
| A、-1或1 | B、1 | C、-1 | D、3 |