题目内容
若a，b∈R，则“|a|＞|b|成立”是“a2＞b2成立”的（ ）
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充要条件 |
| D、既非充分又非必要条件 |
考点：必要条件、充分条件与充要条件的判断
专题：简易逻辑
分析：根据不等式的性质，利用充分条件和必要条件的定义即可得到结论．
解答：
解：若|a|＞|b|，则|a|2＞|b|2成立，即a2＞b2成立，
若a2＞b2成立，则等价为|a|2＞|b|2成立，即|a|＞|b|成立，
∴“|a|＞|b|成立”是“a2＞b2成立”的充要条件．
故选：C
若a2＞b2成立，则等价为|a|2＞|b|2成立，即|a|＞|b|成立，
∴“|a|＞|b|成立”是“a2＞b2成立”的充要条件．
故选：C
点评：本题主要考查充分条件和必要条件的判断，利用不等式的性质是解决本题的关键．
练习册系列答案
相关题目
空气质量指数PM2.5（单位：μg/m3）表示每立方米空气中可入肺颗粒物的含量，这个值越高，就代表空气污染越严重：执行如图所示的程序框图，若输入n的值为7，则输出s的值是（ ）
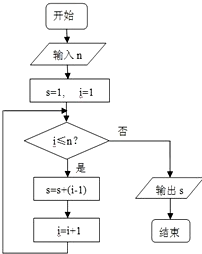
| A、10 | B、16 | C、22 | D、17 |
已知向量
=（1，m），
=（m，2），若
⊥
，则实数m的值为（ ）
| a |
| b |
| a |
| b |
A、-
| ||
B、
| ||
C、±
| ||
| D、0 |
已知实数x∈[1，10]，执行如图所示的流程图，则输出的x不小于63的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
若某程序框图如图所示，则该程序运行后输出的值是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|