题目内容
10.已知Sn是数列{an}的前n项和,且Sn+1=Sn+an+3,a4+a5=23,则S8=( )| A. | 72 | B. | 88 | C. | 92 | D. | 98 |
分析 利用已知条件判断数列是等差数列,然后利用等差数列的性质求和求解即可.
解答 解:Sn是数列{an}的前n项和,且Sn+1=Sn+an+3,
可得an+1=an+3,
所以数列{an}是等差数列,公差为3,
a4+a5=23,
S8=4(a4+a5)=92.
故选:C.
点评 本题考查等差数列的判断,数列的递推关系式的应用,等差数列的性质的应用,考查计算能力.

练习册系列答案
相关题目
20.复数z1,z2在复平面内对应的点的坐标分别为(0,2),(1,-1),则$\frac{z_1}{z_2}$的模为( )
| A. | 1 | B. | 1+i | C. | $\sqrt{2}$ | D. | 2 |
18.a,b,c表示直线,M表示平面,给出下列四个命题:
①若a∥M,b∥M,则a∥b;
②若b?M,a∥b,则a∥M;
③若a⊥c,b⊥c,则a∥b;
④若a⊥M,b⊥M,则a∥b.
其中正确的命题的个数是( )
①若a∥M,b∥M,则a∥b;
②若b?M,a∥b,则a∥M;
③若a⊥c,b⊥c,则a∥b;
④若a⊥M,b⊥M,则a∥b.
其中正确的命题的个数是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
5.幂函数f(x)=(m2-m-1)x5m+3在(0,+∞)上是增函数,则m=( )
| A. | 2 | B. | -1 | C. | 4 | D. | 2或-1 |
2.已知两定点A(-1,0)和B(1,0),动点P(x,y)在直线l:y=x+3上移动,椭圆C以A,B为焦点且经过点P,则椭圆C的离心率的最大值为( )
| A. | $\frac{\sqrt{5}}{5}$ | B. | $\frac{\sqrt{10}}{5}$ | C. | $\frac{2\sqrt{5}}{5}$ | D. | $\frac{2\sqrt{10}}{5}$ |
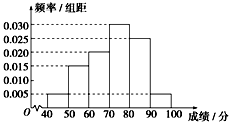 某校从参加高二年级学业水平测试的学生中抽出80名学生,其数学成绩 (均为整数)的频率分布直方图如图所示.估计这次测试中数学成绩的平均分为72,众数为75.
某校从参加高二年级学业水平测试的学生中抽出80名学生,其数学成绩 (均为整数)的频率分布直方图如图所示.估计这次测试中数学成绩的平均分为72,众数为75.