题目内容

15．函数$y=\frac{（2-x）{e}^{x}}{（x-1）^{2}}$的图象大致为（　　）
A．B．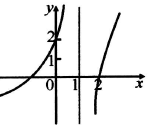
C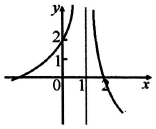．D．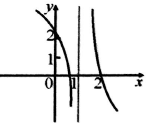

分析 分析函数令$y=\frac{（2-x）{e}^{x}}{（x-1）^{2}}$的零点个数，利用排除法，可得函数图象．

解答 解：令$y=\frac{（2-x）{e}^{x}}{（x-1）^{2}}$=0，则x=2，
故函数只有一个零点2，
故排除B，C，D，
故选：A．

点评 本题考查的知识点是函数的图象，函数的零点，难度不大，属于基础题．

练习册系列答案
相关题目
5．若a=logπ3，b=log3π，c=lnπ，则（　　）
A．c＞a＞bB．b＜c＜aC．a＜b＜cD．a＜c＜b
6．给出下列命题：
①函数y=sin2x偶函数； 
②函数y=sin2x的最小正周期为π；
③函数y=ln（x+1）没有零点；  
④函数y=ln（x+1）在区间（-1，0）上是增函数．
其中正确的命题是②④（只填序号）
3．已知三棱锥P-ABC的顶点都在同一个球面上（球O），且PA=2，PB=PC=$\sqrt{6}$，当三棱锥P-ABC的三个侧面的面积之和最大时，该三棱锥的体积与球O的体积的比值是$\frac{3}{16π}$．
10．已知Sn是数列{an}的前n项和，且Sn+1=Sn+an+3，a4+a5=23，则S8=（　　）
A．72B．88C．92D．98
20．已知命题p：?x∈（-∞，0），2x＜3x；命题q：?x∈（0，$\frac{π}{2}$），sinx＜x，则下列命题为真命题的是（　　）
A．p∧qB．p∨（￢q）C．（￢p）∧qD．p∧（￢q）
7．已知数列{an}的前n项和为Sn，若4Sn=（2n-1）an+1+1，a1=1．
（1）求数列{an}的通项公式；
（2）令${b_n}=\frac{n+1}{{{{（n+2）}^2}{{（{a_n}+1）}^2}}}$，数列{bn}的前n项和为Tn，证明：对于任意的n∈N*，都有${T_n}＜\frac{5}{64}$．
4．已知函数f（x）是定义在R上的偶函数，且在区间[0，+∞）单调递增．若实数a满足f（log2a）+f（log${\;}_{\frac{1}{2}}$a）＜2f（1），则a的取值范围（　　）
A．[1，2]B．（0，$\frac{1}{2}$]C．（$\frac{1}{2}$，2）D．（0，2]
5．函数y=x-1在区间[1，2]上的最大值是1．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网