题目内容
19.已知圆C的面积被直线y=x平分,且圆C过点(2,0),则该圆面积最小时的圆方程为(x-1)2+(y-1)2=2.分析 由题意,(2,0)到直线y=x的距离为圆的半径,即$\frac{2}{\sqrt{2}}$=2,此时圆心坐标为y=x与直线y=-x+2的交点,即(1,1),可得该圆面积最小时的圆方程.
解答 解:由题意,(2,0)到直线y=x的距离为圆的半径,即$\frac{2}{\sqrt{2}}$=$\sqrt{2}$,
此时圆心坐标为y=x与直线y=-x+2的交点,即(1,1),
∴该圆面积最小时的圆方程为(x-1)2+(y-1)2=2,
故答案为(x-1)2+(y-1)2=2.
点评 本题考查圆的方程,考查直线与圆的位置关系,属于中档题.

练习册系列答案
相关题目
10.已知Sn是数列{an}的前n项和,且Sn+1=Sn+an+3,a4+a5=23,则S8=( )
| A. | 72 | B. | 88 | C. | 92 | D. | 98 |
14.设全集U=R,集合A={y|y=x2-2},B={x|x≥3},则A∩(∁UB)=( )
| A. | ∅ | B. | {x|x≤-2} | C. | {x|x<3} | D. | {x|-2≤x<3} |
4.已知函数f(x)是定义在R上的偶函数,且在区间[0,+∞)单调递增.若实数a满足f(log2a)+f(log${\;}_{\frac{1}{2}}$a)<2f(1),则a的取值范围( )
| A. | [1,2] | B. | (0,$\frac{1}{2}$] | C. | ($\frac{1}{2}$,2) | D. | (0,2] |
8.cos10°•cos20°-cos80°•sin20°=( )
| A. | $\frac{1}{2}$ | B. | cos10° | C. | $\frac{{\sqrt{3}}}{2}$ | D. | -sin10° |
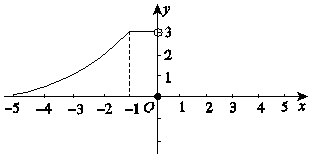
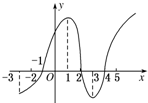 如图所示是y=f(x)的导数图象,则下列判断中正确结论的序号是②④.
如图所示是y=f(x)的导数图象,则下列判断中正确结论的序号是②④.