题目内容
20.若l,m表示两条不相同的直线,α,β是两个不同的平面,则下列命题中为真命题的是①④(填所有正确答案的序号).①若l⊥m,l⊥α,m⊥β,则α⊥β; ②若l⊥m,l?α,m?β,则α⊥β;
③若l⊥β,α⊥β,则l∥α; ④若l∥m,l⊥α,m?β,则α⊥β.
分析 对4个命题分别进行判断,即可得出结论.
解答 解:①l⊥m,l⊥α,m⊥β,必有α⊥β,①正确.
②由两平面垂直的判定定理,知②不正确.
③若l⊥β,α⊥β,则l∥α或l?α,不正确;
④若l∥m,l⊥α,则m⊥α,∵m?β,∴α⊥β,正确.
故答案为①④.
点评 本题主要考查线面与面面平行以及垂直的判定定理以及性质定理,是对课本知识的综合考查.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
10.已知Sn是数列{an}的前n项和,且Sn+1=Sn+an+3,a4+a5=23,则S8=( )
| A. | 72 | B. | 88 | C. | 92 | D. | 98 |
8.cos10°•cos20°-cos80°•sin20°=( )
| A. | $\frac{1}{2}$ | B. | cos10° | C. | $\frac{{\sqrt{3}}}{2}$ | D. | -sin10° |
15.已知△ABC中,sinA+2sinBcosC=0,则tanA的最大值是( )
| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\frac{{2\sqrt{3}}}{3}$ | C. | $\sqrt{3}$ | D. | $\frac{{4\sqrt{3}}}{3}$ |
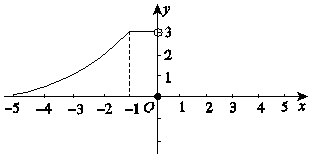
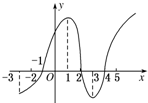 如图所示是y=f(x)的导数图象,则下列判断中正确结论的序号是②④.
如图所示是y=f(x)的导数图象,则下列判断中正确结论的序号是②④.