题目内容
16.x、y满足约束条件$\left\{\begin{array}{l}{x≥1}\\{x+y≥3}\\{2x+y≥6}\end{array}\right.$,若z=ax+y有最小值6,则实数a=( )| A. | -4 | B. | -2 | C. | 2 | D. | 4 |
分析 作出可行域,变形目标函数,分类讨论并数形结合平移直线可得结论.
解答 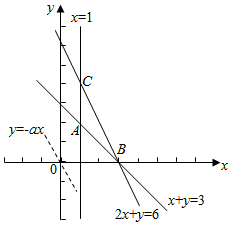 解:作出约束条件$\left\{\begin{array}{l}{x≥1}\\{x+y≥3}\\{2x+y≥6}\end{array}\right.$所对应的可行域(如图△ABC),
解:作出约束条件$\left\{\begin{array}{l}{x≥1}\\{x+y≥3}\\{2x+y≥6}\end{array}\right.$所对应的可行域(如图△ABC),
变形目标函数可得y=-ax+z,
当-a>0即a<0时,直线经过点B(3,0)时,直线截距最小值,
目标函数z取最小值,故3a=6,解得a=2,舍去;
当-a<0即a>0时,直线经过点A(1,2)时,直线截距最小值,
目标函数z取最小值,故a+2=6,解得a=4.
故选:D.
点评 本题考查简单线性规划,准确作图并数形结合是解决问题的关键,属中档题.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
7.设(3$\root{3}{x}$+$\frac{1}{\sqrt{x}}$)n的展开式中的各项系数之和为P,而它的二项式系数之和为S.若P+S=272,那么展开式中x-2项的系数是( )
| A. | 1 | B. | 12 | C. | 54 | D. | 81 |
8.将离心率为e1的双曲线C1的实半轴长a和虚半轴长b同时增加m (m>0)个单位长度,得到离心率为e2的双曲线C2,则当a<b时有( )
| A. | e1>e2 | B. | e1<e2 | C. | e1≤e2 | D. | e1≥e2 |