题目内容
8.将离心率为e1的双曲线C1的实半轴长a和虚半轴长b同时增加m (m>0)个单位长度,得到离心率为e2的双曲线C2,则当a<b时有( )| A. | e1>e2 | B. | e1<e2 | C. | e1≤e2 | D. | e1≥e2 |
分析 运用离心率公式和a,b,c的关系,结合a<b则$\frac{b}{a}$>$\frac{b+m}{a+m}$,可得e1,e2的大小关系.
解答 解:设e1=$\frac{c}{a}$=$\frac{\sqrt{{a}^{2}+{b}^{2}}}{a}$=$\sqrt{1+\frac{{b}^{2}}{{a}^{2}}}$,
由题意可得e2=$\sqrt{1+(\frac{b+m}{a+m})^{2}}$,
由a<b可得$\frac{b}{a}$>$\frac{b+m}{a+m}$,
即有e1>e2,
故选:A.
点评 本题考查双曲线的离心率的大小比较,注意运用离心率公式和不等式的性质,考查运算能力,属于基础题.

练习册系列答案
相关题目
16.x、y满足约束条件$\left\{\begin{array}{l}{x≥1}\\{x+y≥3}\\{2x+y≥6}\end{array}\right.$,若z=ax+y有最小值6,则实数a=( )
| A. | -4 | B. | -2 | C. | 2 | D. | 4 |
19.双曲线4x2-y2=1的一条渐近线的方程为( )
| A. | 2x+y=0 | B. | 2x+y=1 | C. | x+2y=0 | D. | x+2y=1 |
13.经过点(3,-$\sqrt{2}$)的双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1,其一条渐近线方程为y=$\frac{\sqrt{3}}{3}$x,该双曲线的焦距为( )
| A. | $\sqrt{2}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | 4 |
20.若双曲线C:x2-$\frac{{y}^{2}}{{b}^{2}}$=1(b>0)的顶点到渐近线的距离为$\frac{\sqrt{2}}{2}$,则双曲线的离心率e=( )
| A. | 2 | B. | $\sqrt{2}$ | C. | 3 | D. | $\sqrt{3}$ |
18.经过点(2,1),且渐近线与圆x2+(y-2)2=1相切的双曲线的标准方程为( )
| A. | $\frac{{x}^{2}}{\frac{11}{3}}$-$\frac{{y}^{2}}{11}$=1 | B. | $\frac{{x}^{2}}{2}$-y2=1 | C. | $\frac{{y}^{2}}{\frac{11}{3}}$-$\frac{{x}^{2}}{11}$=1 | D. | $\frac{{y}^{2}}{11}$-$\frac{{x}^{2}}{\frac{11}{3}}$=1 |

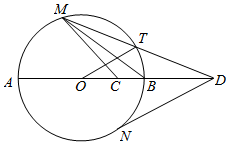 如图,AB是圆O的直径,C是半径OB的中点,D是OB延长线上一点,且BD=OB,直线MD与圆O相交于点M,T(不与A,B重合),DN与圆O相切于点N,连结MC,MB,OT
如图,AB是圆O的直径,C是半径OB的中点,D是OB延长线上一点,且BD=OB,直线MD与圆O相交于点M,T(不与A,B重合),DN与圆O相切于点N,连结MC,MB,OT