题目内容
1.已知函数f(x)=1+lnx-aex(Ⅰ)若曲线y=f(x)在x=1处的切线与x轴平行,求实数a的值;
(Ⅱ)若对任意x∈(0,+∞),不等式f(x)≤0恒成立,求实数a的取值范围.
分析 (Ⅰ)根据导数和几何意义即可求出,
(Ⅱ)分离参数,构造函数,利用导数,求出函数的最值,即可求出参数的取值范围
解答 解:(Ⅰ)∵f(x)=1+lnx-aex,
∴f′(x)=$\frac{1}{x}$-aex,x∈(0,+∞).
由于曲线y=f(x)在x=1处的切线与x轴平行,
∴f′(1)=1-ae=0,
解得$a=\frac{1}{e}$,
(Ⅱ)由条件知对任意x∈(0,+∞),不等式f(x)≤0恒成立,
此命题等价于a≥$\frac{1+lnx}{{e}^{x}}$对任意x∈(0,+∞)恒成立
令$h(x)=\frac{1+lnx}{e^x}$,x∈(0,+∞).
∴${h^'}(x)=\frac{{\frac{1}{x}-1-lnx}}{e^x}$=$\frac{1}{{e}^{x}}$($\frac{1}{x}$-1-lnx),x∈(0,+∞).
令g(x)=($\frac{1}{x}$-1-lnx),x∈(0,+∞).
则g′(x)=-$\frac{1}{{x}^{2}}$-$\frac{1}{x}$<0.
∴函数g(x)在x∈(0,+∞)上单调递减.
注意到g(1)=0,即x=1是g(x)的零点,
而当x∈(0,1)时,g(x)>0;当x∈(1,+∞)时,g(x)<0.
又ex>0,所以当∈(0,1)时,h′(x)>0;当x∈(1,+∞)时,h′(x)<0.
则当x变化时,h′(x)的变化情况如下表:
| x | (0,1) | 1 | (1,+∞) |
| h′(x) | + | 0 | - |
| h(x) | ↗ | 极大值$\frac{1}{e}$ | ↘ |
点评 本题考查利用函数的最值求参数问题,解题时要认真审题,仔细解答,考查了等价转化思想及导数性质的合理运用,属于难题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.在如图所示的计算1+5+9+…+2013的程序框图中,判断框内应填入( )
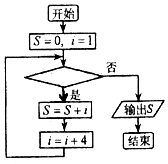

| A. | i≤504 | B. | i≤2009 | C. | i≤2013 | D. | i<2013 |
10.在△ABC中,a,b,c分别为内角A,B,C的对边,且2absinC=$\sqrt{3}$(b2+c2-a2),若a=$\sqrt{13}$,c=3,则△ABC的面积为( )
| A. | 3 | B. | 3$\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | $\frac{3\sqrt{3}}{2}$ |
6.已知α∈($\frac{3}{2}$π,2π),且满足cos(α+$\frac{2017}{2}$π)=$\frac{3}{5}$,则sinα+cosα=( )
| A. | -$\frac{7}{5}$ | B. | -$\frac{1}{5}$ | C. | $\frac{1}{5}$ | D. | $\frac{7}{5}$ |