题目内容
2．设命题p：实数x满足x2-4ax+3a2＜0，其中a＜0；命题q：实数x满足|2x+7|＜5，（1）当a=-1时，若p∧q为真，求x范围；
（2）若￢p是￢q的必要不充分条件，求实数a的取值范围．
分析 （1）分别化简p，q，根据p∧q为真，则p真且q真，即可得出；
（2）?p是?q的必要不充分条件，则q是p的必要不充分条件，即可得出．
解答 解：（1）当a=-1时，p真，则x2+4x+3＜0，解得-3＜x＜-1；
q真，则-5＜2x+7＜5，解得-6＜x＜-1．
∵p∧q为真，则p真且q真，
故x范围为（-3，-1）．
（2）?p是?q的必要不充分条件，则q是p的必要不充分条件，
∵p真，有3a＜x＜a，
∴$\left\{\begin{array}{l}a≤-1\\ 3a≥-6\end{array}\right.$，
故-2≤a≤-1．
点评 本题考查了不等式的解法、简易逻辑的判定方法，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
13．如图，平行六面体ABCD-A1B1C1D1中，AC与BD交于点M，设$\overrightarrow{AB}=\overrightarrow a，\overrightarrow{AD}=\overrightarrow b，\overrightarrow{A{A_1}}$=$\overrightarrow c$，则$\overrightarrow{{B_1}M}$=（ ）
| A． | $-\frac{1}{2}\overrightarrow a-\frac{1}{2}\overrightarrow b-\overrightarrow c$ | B． | $\frac{1}{2}\overrightarrow a+\frac{1}{2}\overrightarrow b-\overrightarrow c$ | C． | $\frac{1}{2}\overrightarrow a-\frac{1}{2}\overrightarrow b-\overrightarrow c$ | D． | $-\frac{1}{2}\overrightarrow a+\frac{1}{2}\overrightarrow b-\overrightarrow c$ |
工艺扇面是中国书画一种常见的表现形式，某班级想用布料制作一面如图所示的扇面．已知扇面展开的中心角为120°，外圆半径为50cm，内圆半径为20cm，则制作这样的一面扇面需要的布料为2198cm2（用数字作答，π取3.14）．
17．
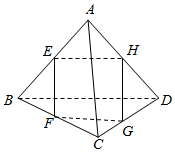在如图所示的空间四边形ABCD中，E、F、G、H分别是AB，BC，CD，AD的中点，则图中共有多少对线面平行关系？（ ）
在如图所示的空间四边形ABCD中，E、F、G、H分别是AB，BC，CD，AD的中点，则图中共有多少对线面平行关系？（ ）| A． | 2对 | B． | 4对 | C． | 6对 | D． | 8对 |