题目内容
17.设f(x)是定义在R上的奇函数,且对任意实数x都有f(x+2)=-f(x),当x∈[0,2]时,f(x)=2x-x2,则f(0)+f(1)+f(2)+…+f(2015)=0.分析 根据条件判断函数的周期性,利用函数奇偶性和周期性的关系进行转化求解即可.
解答 解:∵设f(x)是定义在R上的奇函数,且对任意实数x都有f(x+2)=-f(x),
∴f(x+4)=-f(x+2)=f(x),
∴函数f(x)是周期为4的周期函数,
∵当x∈[0,2]时,f(x)=2x-x2,
∴f(0)=0,f(1)=2-1=1,f(2)=0,f(3)=-1,
∴f(0)+f(1)+f(2)+…+f(2015)=504×[f(0)+f(1)+f(2)+f(3)]=504×(0+1+0-1)=0.
故答案为:0
点评 本题主要考查函数值的计算,根据条件判断函数的周期性是解决本题的关键.

练习册系列答案
相关题目
2.设全集U={0,1,2,3,4},集合A={1,2,3},B={2,3,4},则A∪(∁∪B)=( )
| A. | {0,1,2,3} | B. | {1} | C. | {0,1} | D. | {0} |
9.执行如图所示的程序框图,则输出S的值为( )


| A. | -10 | B. | 6 | C. | 8 | D. | 14 |
6.如图,在正方体ABCD-A1B1C1D1中,M为BB1的中点,则二面角M-CD1-A的余弦值为( )
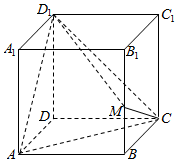

| A. | $\frac{\sqrt{3}}{6}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{6}}{3}$ |
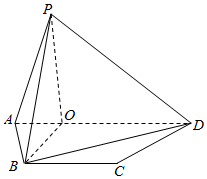 如图,等腰梯形ABCD中,AD∥BC,且P是平面ABCD外一点,P在平面ABCD上的射影O恰在AD上,OB=OP=$\sqrt{3}$OA=$\sqrt{3}$,AB=BC=2.
如图,等腰梯形ABCD中,AD∥BC,且P是平面ABCD外一点,P在平面ABCD上的射影O恰在AD上,OB=OP=$\sqrt{3}$OA=$\sqrt{3}$,AB=BC=2.